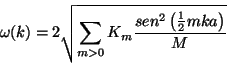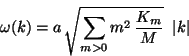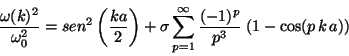Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba

Física Moderna II


Guía N$^{\circ}$7: Vibraciones del Cristal Armónico

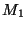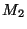Problema 1: Cadena lineal diatómica Considere una cadena lineal en la cual se alternan iones de masa $M_1$ y $M_2$, y sólo interactúan los vecinos más cercanos.
a) Mostrar que la relación de dispersión para los modos normales es:

$$\omega(k)^2 = \frac{K}{M_1 M_2} \left( M_1 + M_2 \pm \sqrt{M_1^2 + M_2^2 + 2 M_1 M_2 \cos(k a)} \right)$$

b) Discutir la forma de la relación de dispersión y la naturaleza de los modos normales cuando 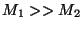$M_1 >> M_2$.
c) Comparar la relación de dispersión obtenida con la de una cadena lineal monoatómica cuando 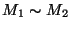$M_1 \sim M_2$.

Problema 2: Cadena Lineal con interacción a m-ésimos vecinos Re-examinar la teoría de las cadenas lineales monoatómicas asumiendo interacciones hasta el m-ésimo vecino; así la ecuación de movimiento para el átomo en la posición 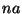$na$ resulta:

$$M \frac{d^2 u(na)}{dt^2} = \sum_{m>0} K_m \left[ u((n+m) a) + u((n-m) a) - 2 u(n a) \right]$$

a) Mostrar que la relación de dispersión debe ser generalizada según:

$$\omega(k) = 2 \sqrt{\sum_{m>0} K_m \frac{sen^2 \left( \frac{1}{2} m k a \right)}{M}}$$

b) Mostrar que en el límite de longitudes de onda larga se tiene que:

$$\omega(k) = a \,\sqrt{\sum_{m>0} m^2 \,\frac{K_m}{M}} \;\; \vert k\vert$$

asumiendo que 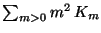$\sum_{m>0} m^2 \, K_m$ converge.

Problema 3: Cristal iónico unidimensional Considere una cadena de iones de igual masa y cargas 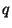$q$ de signos alternados. El potencial interatómico será suma de dos contribuciones:
a) Una de corto alcance (vecinos cercanos) y constante de fuerza 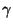$\gamma$,
b) una interacción coulombiana entre los iones. Mostrar que la contribución de la interacción coulombiana a la constante de fuerza atómica es:

$$C_p = \frac{2 (-1)^p q^2}{p^3 a^3}$$

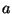donde $a$ es la distancia entre primeros vecinos.
Mostrar tambien que la relaciónde dispersión puede ser escrita como:

$$\frac{\omega(k)^2}{\omega_0^2} = sen^2 \left( \frac{k a}{2}... ... \sum_{p=1}^{\infty} \frac{(-1)^p}{p^3} \;(1 - \cos(p\,k\,a))$$

donde:

$$\omega_0^2 = \frac{4 \gamma}{M} \;\; y \;\;\; \sigma = \frac{q^2}{\gamma a^3}$$

Problema 4: Calor específico de un sólido bidimensional
a) Construya una expresión para el calor específico debido a los fonones en un sólido bidimensional que obedece al esquema de Debye y analice el comportamiento a bajas y altas temperaturas.
b) Determine la contribución al calor específico del sólido bidimensional debida a los electrones, asumiendo el modelo de electrón libre.
c) Determine la temperatura para la cual son comparables los calores específicos electrónicos y de red. Confronte con el caso tridimensional.

Fa.M.A.F ©1995