Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Física General IV: Óptica
Guía N 2: Óptica Geométrica I
2: Óptica Geométrica I
Problema 1: Se desea construir un óvalo cartesiano
tal que los puntos conjugados estén separados por 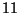 cm cuando
el objeto está a
cm cuando
el objeto está a 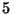 cm del vértice.
Si
cm del vértice.
Si 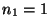 y
y
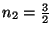 , trace varios puntos pertenecientes
a la superficie requerida.
, trace varios puntos pertenecientes
a la superficie requerida.
Problema 2: Por medio de un diagrama, construya una
lente negativa elíptica-esférica mostrando de que forma pasan
a través de la lente, los rayos y los frentes de onda.
Realice la misma construcción para una lente positiva
oval-esférica.
Problema 3: Utilizando la Ley de Snell, demuestre que
para una superficie esférica de radio 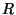 , que separa dos medios de
índices
, que separa dos medios de
índices 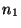 y
y 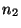 (
(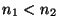 ), en la aproximación
paraxial se cumple:
), en la aproximación
paraxial se cumple:
donde 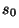 y
y 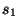 son las distancias de los puntos conjugados al
vértice de la superficie, en los medios
son las distancias de los puntos conjugados al
vértice de la superficie, en los medios 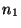 y
y 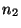 respectivamente.
respectivamente.
Problema 4: Localice la imagen de un objeto colocado
a 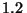 m del vértice de una bola de cristal de
m del vértice de una bola de cristal de 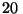 cm de
diámetro (
cm de
diámetro (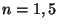 ).
).
Problema 5: Pruebe que la separación mínima
entre los puntos conjugados, objeto real e imagen, para una
lente delgada positiva es 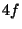 .
.
Problema 6: Una lente bicóncava (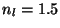 ) tiene
radios de
) tiene
radios de 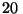 cm y
cm y 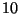 cm y un espesor axial de
cm y un espesor axial de 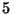 cm. Describa
la imagen de un objeto de
cm. Describa
la imagen de un objeto de 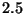 cm de alto colocado a
cm de alto colocado a 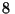 cm del
primer vértice.
cm del
primer vértice.
Problema 7: Un objeto de 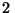 cm de alto se coloca a
cm de alto se coloca a
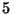 cm a la derecha de una lente delgada positiva de
cm a la derecha de una lente delgada positiva de 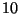 cm de
distancia focal. Describa completamente la imagen resultante.
cm de
distancia focal. Describa completamente la imagen resultante.
Problema 8: ¿Cuál debe ser la distancia focal de
una lente delgada negativa, a fin de que se forme una imagen virtual a
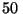 cm de la lente, de una hormiga que está a una distancia de
cm de la lente, de una hormiga que está a una distancia de
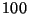 cm? Dado que la hormiga está a la derecha de la lente,
localice y describa la imagen.
cm? Dado que la hormiga está a la derecha de la lente,
localice y describa la imagen.
Problema 9: Determine la distancia focal de una lente
plano-concava (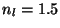 ) que tiene un radio de curvatura de
) que tiene un radio de curvatura de
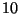 cm. ¿Cuál es su potencia en dioptrías?
cm. ¿Cuál es su potencia en dioptrías?
Problema 10: Escriba una expresión para la distancia
focal 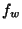 de una lente delgada sumergida en agua (
de una lente delgada sumergida en agua (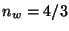 ), en
téminos de su distancia focal cuando está en aire (
), en
téminos de su distancia focal cuando está en aire (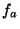 ).
).
Problema 11: Una lente delgada equiconvexa 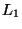 está cementada en contacto íntimo con una lente negativa
está cementada en contacto íntimo con una lente negativa
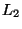 , de forma tal que la combinación tiene una distancia focal
de
, de forma tal que la combinación tiene una distancia focal
de 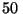 cm en aire. Si sus índices son
cm en aire. Si sus índices son 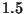 y
y 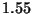 ,
respectivamente, y si la distancia focal de
,
respectivamente, y si la distancia focal de 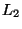 es
es 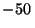 cm,
determine todos los radios de curvatura.
cm,
determine todos los radios de curvatura.
|
Problema 12:
Trace un esquema localizando aproximadamente el diafragma de abertura y
las pupilas de entrada y salida para las lentes de la figura.
|
|
Problema 13: Se muestra en la figura un sistema de
lentes (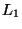 ,
,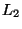 ), un objeto y las pupilas apropiadas.
Configure gráficamente la posición y abertura precisas de las
pupilas y localice la imagen mediante un diagrama.
), un objeto y las pupilas apropiadas.
Configure gráficamente la posición y abertura precisas de las
pupilas y localice la imagen mediante un diagrama.
Problema 14: Trace un diagrama de rayos, localizando
las imágenes de una fuente puntual formadas por un par de espejos
a 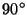 . Realice la misma tarea considerando que el objeto es
una flecha no paralela a la superficie de ninguno de los espejos.
. Realice la misma tarea considerando que el objeto es
una flecha no paralela a la superficie de ninguno de los espejos.
Problema 15: Dos espejos planos forman un ángulo
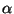 . Aplicando la ley de reflexión, demuestre que cualquier
rayo, cuyo plano de incidencia sea perpendicular a la línea de
intersección, se desvía en las dos reflexiones un ángulo
independiente del de incidencia. Exprese esta desviación en
función de
. Aplicando la ley de reflexión, demuestre que cualquier
rayo, cuyo plano de incidencia sea perpendicular a la línea de
intersección, se desvía en las dos reflexiones un ángulo
independiente del de incidencia. Exprese esta desviación en
función de 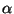 .
.
Problema 16: Un espejo esférico-cóncavo forma la
imagen de una rosa en una pantalla a 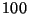 cm de distancia. Si la
rosa está a
cm de distancia. Si la
rosa está a 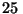 cm del espejo, determine su radio de curvatura.
cm del espejo, determine su radio de curvatura.
Problema 17: Suponga que tiene un espejo
esférico-cóncavo de 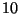 cm de distancia focal.
¿A qué distancia se debe colocar un objeto si su imagen debe ser
derecha y una vez y media más grande?
¿Cuál es el radio de curvatura del espejo?
cm de distancia focal.
¿A qué distancia se debe colocar un objeto si su imagen debe ser
derecha y una vez y media más grande?
¿Cuál es el radio de curvatura del espejo?
Problema 18:
a) Observando la configuración de la imagen, determine la
forma del espejo que cuelga en el fondo del cuadro de van Eyck:
John Arnolfini y su esposa.
b) En la pintura de Velásquez: Venus y Cupido, se
encuentra la Venus observándose a sí misma en el espejo?
Explique.
c) En al pintura de Manet: El Bar del Folies Bergères,
se refleja en un gran espejo detrás de la camarera, un hombre quien
parece estar hablando con ella. Manet intenta dar la sensación de
que el observador ocupa delante del cuadro la posición del hombre
reflejado en el espejo de la pintura. ¿Cuál es el error según
las leyes de la óptica?
Problema 19: Determine la abertura numérica de una
fibra óptica recubierta, sabiendo que el núcleo tiene un
índice igual a 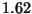 y la cubierta igual a
y la cubierta igual a 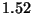 .
¿Cuál es el máximo ángulo de aceptación cuando está
sumergida en aire? ¿Qué ocurrirá con un rayo incidente a
.
¿Cuál es el máximo ángulo de aceptación cuando está
sumergida en aire? ¿Qué ocurrirá con un rayo incidente a
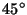 ?
?
Fa.M.A.F ©1997
Pedro Pury
2001-02-14
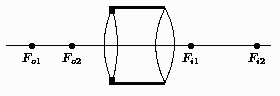
![\begin{picture}(120.00,71.00)
\put(-5.00,40.00){\line(1,0){120.00}}
\bezier{18...
...kebox(0,0)[cc]{$L_2$}}
\put(63.00,20.00){\makebox(0,0)[bc]{A.S.}}
\end{picture}](img33.gif)