Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Física General IV: Óptica
Guía N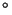 5: Ondas Electromagnéticas -
Polarización
5: Ondas Electromagnéticas -
Polarización
Problema 1: Considere una onda electromagnética
plana, dada por las expresiones (en unidades del SI):
a) ¿Cuál es la frecuencia, longitud de onda, dirección del
movimiento, amplitud, ángulo de fase inicial y polarización de la
onda?
b) Escribir una expresión para la densidad de flujo
magnético.
Problema 2: Escribir una expresión para los campos
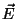 y
y 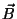 correspondientes a una onda armónica plana
que viaja en la dirección
correspondientes a una onda armónica plana
que viaja en la dirección 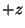 . La onda se encuentra linealmente
polarizada, y su plano de vibración forma un ángulo de
. La onda se encuentra linealmente
polarizada, y su plano de vibración forma un ángulo de
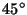 con el plano
con el plano 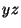 .
.
Problema 3: El promedio temporal de una función
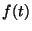 sobre un intervalo
sobre un intervalo 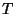 está dado por:
está dado por:
donde 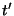 es una variable muda. Si
es una variable muda. Si
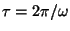 (período de la onda), mostrar que:
(período de la onda), mostrar que:
cuando 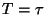 y cuando
y cuando 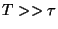 .
.
Problema 4: Una onda electromagnética plana,
linealmente polarizada, que viaja en la dirección 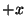 y su plano
de vibración es el
y su plano
de vibración es el 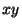 , tiene una frecuencia de
, tiene una frecuencia de 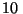 MHz y su
amplitud es
MHz y su
amplitud es 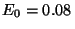 V/m.
V/m.
a) Calcular el período y longitud de onda de la
perturbación.
b) Escribir una expresión para 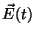 y
y 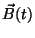 .
.
c) Calcular la densidad de flujo 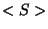 , o irradiancia de la
onda.
, o irradiancia de la
onda.
Problema 5: Un láser de 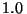 mW tiene un haz cuyo
diámetro es de
mW tiene un haz cuyo
diámetro es de 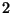 mm. Suponiendo despreciable la divergencia del
haz, calcular la densidad de energía en el seno del haz láser.
mm. Suponiendo despreciable la divergencia del
haz, calcular la densidad de energía en el seno del haz láser.
Problema 6: Utilizando el argumento de la
conservación de la energía demuestre que la amplitud de una
onda cilíndrica debe variar inversamente con 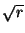 .
.
Problema 7: Si la amplitud del campo eléctrico de la
luz que se propaga en un vidrio de 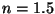 es
es 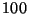 V/m, cuál es
la amplitud de campo magnético? ¿Cuál es la magnitud del vector
de Poynting?
V/m, cuál es
la amplitud de campo magnético? ¿Cuál es la magnitud del vector
de Poynting?
Problema 8: Una onda de luz, armónica, plana y
linealmente polarizada tiene una intensidad de campo eléctrico dada
por:
mientras se propaga dentro de una pieza de vidrio. Calcular:
a) la frecuencia de la luz,
b) su longitud de onda,
c) el índice de refracción del vidrio.
Problema 9: Considerar una placa de vidrio
no-absorbente, cuyo índice es 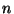 y su espesor
y su espesor  ,
dispuesta transversalmente entre una fuente S y un observador P.
La distancia entre S y P es
,
dispuesta transversalmente entre una fuente S y un observador P.
La distancia entre S y P es 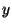 .
.
a) Si la onda no obstruída (sin la placa presente)
observada por P, está descripta por:
mostrar que en presencia de la placa en P se observa:
b) Mostrar que si 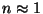 o bien
o bien  es muy
pequeño, entonces
es muy
pequeño, entonces
generado por los osciladores en la placa de vidrio.
Problema 10: Mostrar que para substancias de baja
densidad como los gases, que poseen una única frecuencia de
resonancia 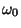 , el índice de refracción viene dado por:
, el índice de refracción viene dado por:
Problema 11: La fucsina es una anilina, la cual
en solución con alcohol tiene un color rojo profundo. Aparece roja
porque absorbe la componente verde del espectro (Como es de
esperarse, la superficie del cristal de fucsina refleja la luz verde
de una manera particularmente marcada). Considerar un prisma hueco de
paredes muy delgadas lleno con esta solución. ¿Cómo lucirá el
espectro emergente del prisma, cuando la luz incidente es blanca?
Problema 12: Describir completamente el estado de
polarización de las siguientes ondas:
a)
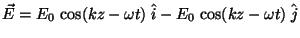
b)
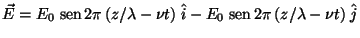
c)
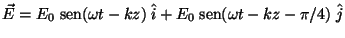
d)
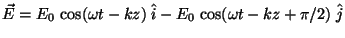
Problema 13: Considerar una perturbación descripta
por la expresión:
¿Qué tipo de onda es? Trazar un diagrama con las principales
características.
Problema 14: Mostrar analíticamente que la
superposición de ondas con estados de polarización 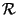 y
y
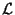 y diferentes amplitudes, genera una onda con estado de
polarización
y diferentes amplitudes, genera una onda con estado de
polarización 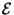 .
.
Problema 15: Escribir una expresión para una onda de
luz con estado de polarización 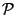 , frecuencia angular
, frecuencia angular
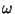 y amplitud
y amplitud 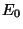 , que se propaga a lo largo del eje
, que se propaga a lo largo del eje 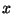 y
cuyo plano de vibración forma un ángulo de
y
cuyo plano de vibración forma un ángulo de 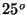 con el plano
con el plano
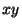 . La perturbación es cero en
. La perturbación es cero en 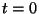 y
y 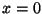 .
.
Problema 16: Suponga que un polarizador ideal es
rotado con un frecuencia angular 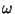 entre dos polarizadores
cruzados ideales fijos. Mostrar que la densidad de flujo emergente
satisface:
entre dos polarizadores
cruzados ideales fijos. Mostrar que la densidad de flujo emergente
satisface:
donde 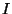 es la densidad de flujo final e
es la densidad de flujo final e 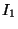 es la densidad de
flujo emergente del primer polarizador.
es la densidad de
flujo emergente del primer polarizador.
Problema 17: Un rayo de luz amarilla incide sobre una
placa de calcita a 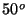 . La placa es cortada de forma tal que el
eje óptico es paralelo a la cara frontal y perpendicular al plano
de incidencia. Encontrar la separación angular entre los dos rayos
emergentes.
. La placa es cortada de forma tal que el
eje óptico es paralelo a la cara frontal y perpendicular al plano
de incidencia. Encontrar la separación angular entre los dos rayos
emergentes.
Problema 18:
El cristal de la fotografia (Figura 8.68 del libro ``Optics'' de
Eugene Hecht (Addison-Wesley, Second Edition, 1987))
es calcita y tiene su punta roma en el lado izquierdo superior. Los
dos polaroides tienen sus ejes de transmisión paralelos a los
bordes cortos. Discutir en detalle lo observado en la figura.
Problema 19:
El cristal de calcita del problema anterior se muestra en la
Figura 8.69 en tres diferentes orientaciones. Su punta roma está a
la izquierda en (a), abajo a la izquierda en (b) y abajo en (c).
El eje de transmisión del polaroid es horizontal. Explicar cada una
de las fotografias, en particular (b).
Fa.M.A.F ©1997
Pedro Pury
2001-02-14
![\begin{displaymath}
\begin{array}{ll}
E_x = & 0 \\
E_y = &
2 \,\cos \left[...
... 10^{14} \,(t-x/c) +\pi/2 \right] \\
E_z = & 0
\end{array}
\end{displaymath}](img2.gif)