La ecuación general para ondas que se propagan
en una dimensión con velocidad ![]() es
es
| (1) |
| (2) |
Para reconocer que rol cumplen las constantes ![]() y
y ![]() imaginemos los siguientes experimentos. En primer lugar,
fijemos un observador en una dada coordenada
imaginemos los siguientes experimentos. En primer lugar,
fijemos un observador en una dada coordenada ![]() y
midamos cuanto tiempo debe transcurrir hasta que dicho
observador vuelve a encortrar el mismo valor para la perturbación
y
midamos cuanto tiempo debe transcurrir hasta que dicho
observador vuelve a encortrar el mismo valor para la perturbación
![]() . Dado que estamos trabajando con una función seno, este
tiempo resulta igual a
. Dado que estamos trabajando con una función seno, este
tiempo resulta igual a
![]() .
Este valor se conoce como período de la oscilación.
En consecuencia,
.
Este valor se conoce como período de la oscilación.
En consecuencia, ![]() es la frecuencia angular y
es la frecuencia angular y
![]() es la frecuencia o
frecuencia temporal del movimiento y representa el número de
oscilaciones completas por unidad de tiempo que realiza el movimiento
ondulatorio periódico en un punto cualquiera del espacio. La unidad
en la que se mide la frecuencia resulta entonces el ciclo por segundo
o Hertz (Hz).
es la frecuencia o
frecuencia temporal del movimiento y representa el número de
oscilaciones completas por unidad de tiempo que realiza el movimiento
ondulatorio periódico en un punto cualquiera del espacio. La unidad
en la que se mide la frecuencia resulta entonces el ciclo por segundo
o Hertz (Hz).
Como segundo experimento mental, congelemos el movimiento en un dado
instante ![]() y midamos la distancia entre dos puntos sobre el eje
y midamos la distancia entre dos puntos sobre el eje
![]() para los cuales
para los cuales ![]() toma el mismo valor. Nuevamente, dado
que trabajamos con una función sinusoidal obtenemos que dicha
distancia es
toma el mismo valor. Nuevamente, dado
que trabajamos con una función sinusoidal obtenemos que dicha
distancia es
![]() y se conoce como longitud de
onda. Así, resulta que
y se conoce como longitud de
onda. Así, resulta que ![]() es el número de onda y
mide el número de oscilaciones completas por unidad de longitud.
De lo expresado en la Ec. (3), obtenemos la relación
que víncula a
es el número de onda y
mide el número de oscilaciones completas por unidad de longitud.
De lo expresado en la Ec. (3), obtenemos la relación
que víncula a ![]() ,
, ![]() y
y ![]()
Si se superponen ondas la función resultante es la suma de las
correspondientes funciones de onda. Este principio de superposición
da lugar a la existencia de ondas estacionarias. A tal fin,
supongamos que tenemos dos ondas armónicas en fase y de igual
amplitud pero viajando en sentidos opuestos:
| (5) |
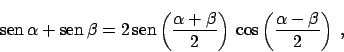 |
(6) |