Práctico de Laboratorio N
Objetivo: Observación cuantitativa de los patrones de difracción de Fraunhofer de rendijas alargadas, aberturas rectangulares, circulares y obstaculos opacos.
Introducción: Según el principio de Huygens-Fresnel, cada punto no obstruído de un frente de ondas actúa como centro emisor de ondas esféricas secundarias (con igual frecuencia que la de la onda primaria). La amplitud del campo eléctrico en todo punto por delante, está dada por la superposición de todas las ondas secundarias.
En el caso de obstáculos opacos, su efecto puede visualizarse de igual manera, excepto por el signo, substituyendo la onda incidente y sus ondas secundarias (provenientes de todos los puntos no obstruídos) por el campo generado sólo por las ondas secundarias que se habrían generado en la región del obstaculo, si este no existiera.
Se deben distinguir dos situaciones de observación distintas.
La primera, en la cual el plano se observación está próximo
al plano del obstáculo (sea este opaco o una abertura), se conoce
como condición de Fresnel o de campo cercano.
La segunda, conocida como condición de Fraunhofer o de
campo lejano, se obtiene cuando el plano de observación se aleja
lo suficiente como para cumplir con la condición
Experimentalmente se trabaja con un frente de ondas plano incidente, generado por un láser o colocando una fuente puntual en el foco de una lente convergente. La condición de Fraunhofer se asegura colocando el obstáculo en el foco de una lente positiva, permitiendo así trabajar de forma cómoda con la pantalla a distancia finita del obstáculo, si bien la observación se realiza a distancia infinita.
Para una rendija delgada el patrón de difracción de franjas
paralelas observado es tal que la irradiancia ![]() sobre la pantalla
está dado en función del ángulo de observación
sobre la pantalla
está dado en función del ángulo de observación ![]() por
por
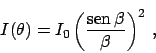 |
(2) |
Para una rendija rectángular el patrón de difracción sobre
la pantalla presenta una irradiancia en cada punto de la
pantalla de coordenadas ![]() (respecto del centro) dada por
(respecto del centro) dada por
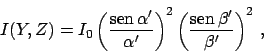 |
(3) |
Para una abertura circular, por otro lado, se tiene que
el patrón de irradiancia en la pantalla en función
del ángulo de observación está dado por
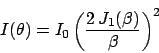 |
(4) |
Desarrollo Experimental:
Experiencia 1:
Observar la imagen de una rendija delgada de ancho conocido,
ilumidada por un láser de He-Ne. Llevar la pantalla a la
proximidad del plano de la rendija y alejarla paulatinamente.
Registrar la distancia a partir de la cual se observan claramente
franjas alrededor de la imagen y la necesaria para ya no poder
distinguir la imagen de la rendija en la pantalla.
Comparar con la condición de Fraunhofer dada en la
Ec. (1).
Experiencia 2:
Reproducir la disposición experimental de Fraunhofer
para la observación de una rendija de ancho conocida.
Determinar la separación entre los mínimos que limitan
el máximo central y determinar la longitud de onda del
láser de He-Ne. Identificar la principal fuente de error.
Experiencia 3:
Reproducir la disposición experimental de Fraunhofer para
la observación de una abertura cuadrada o rectangular.
A partir de la medición de la distancias entre los mínimos
que delimitan el máximo central, determinar las dimenciones de
la abertura.
Experiencia 4:
Reproducir la disposición experimental de Fraunhofer
para la observación de una abertura circular.
A partir de la medición del diámetro del primer mínimo
(anillo que encierra al disco de Airy o máximo central),
determinar el diámetro de la abertura.
Experiencia 5:
Reproducir la disposición experimental de Fraunhofer
para la observación de un objeto delgado opaco
(emplear un cabello o alambre delgado).
Determinar el espesor del obstáculo a partir
del patrón de difracción observado.
Experiencia 6: Reproducir la disposición experimental de Fraunhofer para la observación de una doble rendija de separación y ancho conocidos. Identificar los patrones de difracción e interferencia. Obturar una de las dos rendijas y observar el patrón resultante. Comparar las distancias entre los mínimos que delimitan el máximo central del patrón de difracción en cada caso.
Bibliografía: