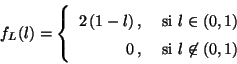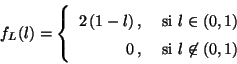Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación
Práctico de Simulación 2000
Problema 1: Un matemático del siglo dieciocho llamado Buffon, sugirió
la siguiente técnica para calcular el valor de 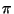 : Tomar una
gran hoja de papel, la cual se encuentra rayada con finas líneas
paralelas separadas entre sí por dos centímetros y arrojar
al azar sobre el papel una fina aguja de un centímetro de largo,
de forma que caiga acostada, un gran número de veces. Se calcula
la proporción de veces que la aguja interseca alguna línea
del papel y el valor de
: Tomar una
gran hoja de papel, la cual se encuentra rayada con finas líneas
paralelas separadas entre sí por dos centímetros y arrojar
al azar sobre el papel una fina aguja de un centímetro de largo,
de forma que caiga acostada, un gran número de veces. Se calcula
la proporción de veces que la aguja interseca alguna línea
del papel y el valor de 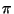 se estima como la inversa de dicha
proporción.
se estima como la inversa de dicha
proporción.
a) Escribir un programa que simule en la computadora
la técnica mencionada de arrojar la aguja. Esto resultará mucho
más cómodo que efectivamente dejar caer una aguja sobre una hoja
rayada. Notar que el problema es equivalente a sortear uniformente la
posición del centro de la aguja en un intervalo de ancho 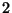 , y
sortear el ángulo que forma la aguja de largo
, y
sortear el ángulo que forma la aguja de largo 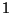 con la
dirección de la recta que contiene al intervalo de interés,
uniformemente entre
con la
dirección de la recta que contiene al intervalo de interés,
uniformemente entre 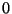 y
y 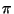 . Para cada prueba verificar a
continuación si la proyección de la aguja sobre la recta
mencionada, interseca algún extremo del intervalo.
. Para cada prueba verificar a
continuación si la proyección de la aguja sobre la recta
mencionada, interseca algún extremo del intervalo.
Realizar una tabla con los valores de 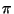 estimados
para un número
estimados
para un número 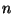 de pruebas, con
de pruebas, con
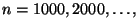
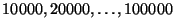 . Estimar el valor de
. Estimar el valor de 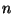 necesario
para asegurar el valor de
necesario
para asegurar el valor de 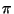 con cinco cifras significativas
(es decir que el error afecte recién al sexto decimal).
con cinco cifras significativas
(es decir que el error afecte recién al sexto decimal).
Nota: Para realizar la simulación el programa
utilizará el valor de 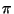 que quiere estimarse. Esto sin
embargo, no constituye un fraude dado que sólo se lo utiliza
para simular el proceso de arrojar la aguja, no en el cálculo
del número en sí.
que quiere estimarse. Esto sin
embargo, no constituye un fraude dado que sólo se lo utiliza
para simular el proceso de arrojar la aguja, no en el cálculo
del número en sí.
b) En base a los conocimientos de la Teoría
de la Probabilidad aprendidos en el curso, elabore un argumento
que explique porqué el método de arrojar la aguja funciona
para estimar el valor de 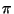 .
.
Problema 2: Presentaremos un versión simplificada de un problema de
interés en el diseño de bases de datos. Consideremos objetos
unidimensionales caracterizados por su longitud 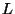 , la cual es una
variable aleatoria continua cuya densidad de probabilidad está dada
por:
, la cual es una
variable aleatoria continua cuya densidad de probabilidad está dada
por:
Supongamos se escogen al azar de manera independiente 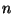 objetos,
cuyas longitudes resultan:
objetos,
cuyas longitudes resultan:
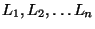 . Estos objetos deben
ser guardados consecutivamente en cajas unidimensionales de
longitud
. Estos objetos deben
ser guardados consecutivamente en cajas unidimensionales de
longitud 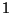 y en el orden de sus correspondientes índices.
Además, ningún objeto puede ser partido en dos cajas.
Esta última condición implica que puede generarse una
gran cantidad de espacio desperdiciado en las cajas utilizadas.
Sea
y en el orden de sus correspondientes índices.
Además, ningún objeto puede ser partido en dos cajas.
Esta última condición implica que puede generarse una
gran cantidad de espacio desperdiciado en las cajas utilizadas.
Sea 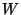 la cantidad de espacio desperdiciado y
la cantidad de espacio desperdiciado y 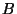 el número de
cajas empleadas para almacenar los
el número de
cajas empleadas para almacenar los 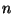 objetos. Obviamente se cumple
que
objetos. Obviamente se cumple
que 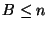 .
.
Para clarificar la notación y las condiciones de
almacenamiento consideremos el siguiente ejemplo:
Supongamos 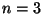 , y
, y 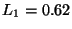 ,
, 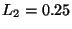 y
y 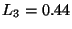 .
Entonces los objetos
.
Entonces los objetos 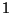 y
y 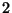 se acomodan en la caja
se acomodan en la caja 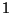 y el
objeto
y el
objeto 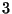 se acomoda en la caja
se acomoda en la caja 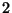 . Se tiene que
. Se tiene que
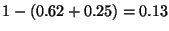 es el espacio vacío en la primer caja
y
es el espacio vacío en la primer caja
y
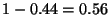 es el espacio desperdiciado en la caja
es el espacio desperdiciado en la caja 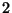 .
Por lo tanto,
.
Por lo tanto,
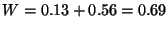 y
y 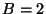 .
.
Asumir 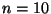 y mediante simulaciones estimar:
y mediante simulaciones estimar:
a) el valor medio y la varianza de 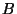 .
.
b) 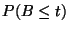 para
para
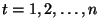 .
.
c) el valor medio del cociente 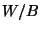 , es decir la
proporción esperada de espacio vacío.
, es decir la
proporción esperada de espacio vacío.
Problema 3: Consideremos un conjunto de 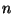 variables aleatorias
independientes e idénticamente distribuídas
variables aleatorias
independientes e idénticamente distribuídas
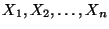 , cuya densidad de probabilidad es
, cuya densidad de probabilidad es
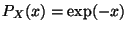 . Consideremos ahora la variable aleatoria:
. Consideremos ahora la variable aleatoria:
Esto es el promedio de las 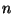 variables dadas.
variables dadas.
a) Construir un histograma para las frecuencias
relativas de la variable aleatoria 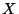 cuya densidad de probabilidad
es
cuya densidad de probabilidad
es 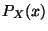 . Sortear 10000 valores de la variable.
. Sortear 10000 valores de la variable.
b) Construir los histogramas de las variables
aleatorias
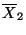 ,
,
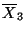 ,
,
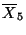 y
y
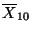 .
Para el calculo de la variable
.
Para el calculo de la variable
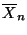 primero debe
sortearse un conjunto de
primero debe
sortearse un conjunto de 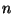 valores de la variable
valores de la variable 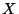 , calcular
un valor de
, calcular
un valor de
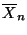 , sortear un nuevo conjunto de
, sortear un nuevo conjunto de 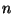 valores de la variable
valores de la variable 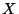 para calcular otro valor de
para calcular otro valor de
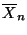 y así sucesivamente hasta tener el
número de valores deseados en el histograma de para la
variable
y así sucesivamente hasta tener el
número de valores deseados en el histograma de para la
variable
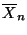 .
.
c) A partir de los datos generados en el item
anterior, calcular el valor medio y la varianza de las variables
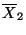 ,
,
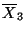 ,
,
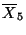 y
y
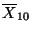 .
.
d) Superponer sobre la gráfica de cada uno de los
histogramas construídos, la curva correspondiente a la densidad
de probabilidad de una variable normal cuya media y varianza son
iguales a las de la variable
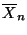 del correspondiente
histograma.
del correspondiente
histograma.
Fa.M.A.F ©2000
Pedro Pury
2000-12-27