Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Guía N 2: Introducción a la Probabilidad
2: Introducción a la Probabilidad
Problema 1: Considere cuatro objetos:
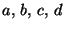 . Suponga
que el orden en el cual se anotan los cuatro objetos
representa
el resultado de un experimento. Sean
. Suponga
que el orden en el cual se anotan los cuatro objetos
representa
el resultado de un experimento. Sean 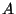 y
y 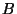 los eventos definidos
como sigue:
los eventos definidos
como sigue:
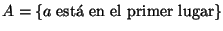 ;
;
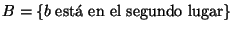 .
.
a) Describir por enumeración el espacio muestral de
este experimento.
b) Describir por enumeración los eventos 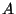 y
y 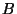 .
.
c) Describir por enumeración los eventos 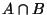 y
y 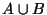 .
.
Problema 2: Sean 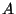 ,
, 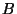 y
y 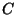 tres eventos asociados con un dado
experimento. Expresar las siguientes proposiciones coloquiales
en notación de conjuntos:
tres eventos asociados con un dado
experimento. Expresar las siguientes proposiciones coloquiales
en notación de conjuntos:
a) Al menos uno de los eventos ocurre.
b) Exactamente uno de los eventos ocurre.
c) Exactamente dos de los eventos ocurren.
d) Ocurren más de dos eventos simultáneamente.
Problema 3:
a) Probar que si 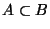 entonces
entonces
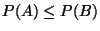 .
.
b)
Si A, B y C son tres eventos, en un espacio de probabilidad,
probar que:
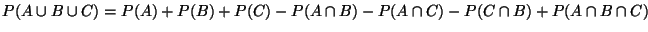 .
.
c) Demostrar que para dos eventos cualesquiera, 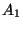 y
y 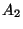 , se tiene que
, se tiene que
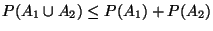 .
.
d) Demostrar que para 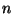 eventos cualesquiera,
eventos cualesquiera,
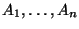 , se tiene que
, se tiene que
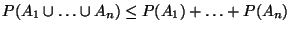 .
Sugerencia: Usar inducción matemática.
Esta desigualdad se llama Desigualdad de Boole.
.
Sugerencia: Usar inducción matemática.
Esta desigualdad se llama Desigualdad de Boole.
e) Demostrar que
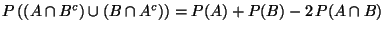 .
Esta probabilidad corresponde al evento en el cual exactamente
uno de los eventos
.
Esta probabilidad corresponde al evento en el cual exactamente
uno de los eventos 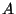 o
o 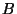 ocurre.
ocurre.
Problema 4: Supóngase que 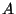 y
y 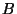 son eventos para los cuales
son eventos para los cuales
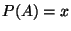 ,
, 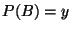 ,
,
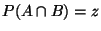 . Expresar cada una de
las probabilidades siguientes en términos de
. Expresar cada una de
las probabilidades siguientes en términos de 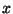 ,
, 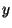 y
y 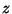 .
.
a)
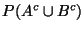
b) 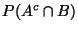
c) 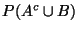
d)
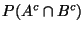
Problema 5: Una instalación cuenta de dos calderas
y un motor.
Sea 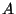 el evento en el cual el motor está en buenas
condiciones;
mientras que los eventos
el evento en el cual el motor está en buenas
condiciones;
mientras que los eventos 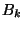 ,
, 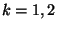 , son los eventos en los
cuales la
, son los eventos en los
cuales la 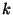 -ésima caldera esté en buenas condiciones.
El evento
-ésima caldera esté en buenas condiciones.
El evento 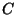 corresponde a que la instalación pueda funcionar.
Si la instalación funciona cada vez que el motor y al menos una
caldera funciona, expresar
corresponde a que la instalación pueda funcionar.
Si la instalación funciona cada vez que el motor y al menos una
caldera funciona, expresar 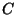 y
y 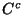 en términos de
en términos de 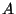 y de
los eventos
y de
los eventos 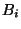 . Interpretar
. Interpretar 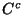 .
.
Problema 6: Existen tres opciones preferidas para cierto
tipo de
automóvil nuevo:
con transmisión automática (A),
con dirección hidráulica (B)
y con radio (C).
Si el 70 % de los compradores eligen la opción (A),
el 80 % eligen la opción (B), el 75 % eligen la opción (C),
el 85 % solicitan A o B, el 90 % solicitan A o C,
el 95 % eligen (B) o (C) y el 98 % eligen (A) o (B) o (C).
Calcular las probabilidades de los siguientes eventos:
a) El siguiente comprador selecciona por lo menos
una de las tres.
b) El siguiente comprador no seleccionará ninguna de
las tres opciones.
c) El siguiente comprador seleccionará sólo uno
con radio.
d) El siguiente comprador seleccionará exactamente
una de las tres opciones.
Asumir que cada comprador elige a su criterio personal,
independientemente de las opciones de los otros compradores.
Problema 7: En una habitación 10 personas tienen
insignias numeradas
del 1 al 10.
Se eligen tres personas al azar y se les pide que dejen la
habitación simultáneamente y se anotan el número de las
insignias.
a) ¿Cuál es la probabilidad de que el menor
número de las insignias sea 5?
b) ¿Cuál es la probabilidad de que el mayor
número de las insignias sea 5?
Problema 8: Diez fichas numeradas de 1 al 10 se mezclan
en una caja.
Se sacan de la caja dos fichas una y otra sin sustitución (X,Y).
¿Cuál es la probabilidad que 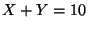 ?
?
Problema 9: Un inspector visita seis máquinas
diferente durante el
día. A fin de impedir que los operadores sepan cuando seran
inspeccionados, se varía el orden de las visitas.
¿De cuántas maneras puede hacerlo?
Problema 10: Utilizando las letras 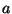 ,
, 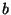 ,
, 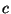 ,
, 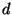 ,
, 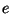 , y
, y 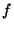 ,
¿cuántas palabras clave de cuatro letras se pueden formar,
si
,
¿cuántas palabras clave de cuatro letras se pueden formar,
si
a) ninguna letra puede aparecer repetida en la
palabra?
b) cualquier letra puede repetirse cualquier
número de veces?
Problema 11:
a) Beethoven escribió 9 sinfonías y Mozart
escribió 27 conciertos para piano. Si el musicalizador de una
radiodifusora desea reproducir primero una sinfonía de Beethoven
y luego un concierto de Mozart, de cuántas maneras se puede
hacer
esto?
b) El gerente de la radiodifusora determina que
en cada noche sucesiva (7 días por semana), se transmitirá
una sinfonía de Beethoven, seguida de un concierto para piano de
Mozart, y luego un cuarteto para cuerdas de Schubert (de los cuales
hay 15).
¿Durante alrededor de cuántos años podría
continuarse este
sistema antes de que tenga que repetirse el mismo programa?
Problema 12: Una caja contiene esferas numeradas
consecutivamente del 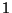 al
al 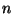 . Se escogen dos esferas al azar. Calcular la probabilidad
de
que los números sobre las esferas sean consecutivos, si
. Se escogen dos esferas al azar. Calcular la probabilidad
de
que los números sobre las esferas sean consecutivos, si
a) las esferas se eligen sin sustitución.
b) las esferas se eligen con sustitución.
Problema 13: Entre los números 1,2,...,50 se escoge
uno al azar.
¿Cuál es la probabilidad de que el número escogido sea
divisible por 6 o por 8?
Problema 14: Un lote contiene 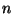 artículos y se sabe que
artículos y se sabe que 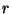 de estos
artículos son defectuosos. Si se inspecciona al azar el lote
completo y en forma sucesiva, cuál es la probabilidad de que
el
de estos
artículos son defectuosos. Si se inspecciona al azar el lote
completo y en forma sucesiva, cuál es la probabilidad de que
el 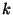 -ésimo artículo
-ésimo artículo 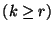 sea el último defectuoso
en el lote?
sea el último defectuoso
en el lote?
Fa.M.A.F ©2002
Pedro Pury
2002-08-09