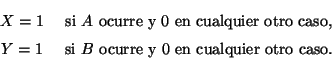Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Guía N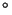 6:
Media, Varianza y Variable Normal
6:
Media, Varianza y Variable Normal
Problema 1: Calcular el valor esperado y la varianza de las variables
aleatorias definidas en los Problemas (2), (6), (9) y (13) de la
Guía N 4.
4.
Problema 2:
a) Calcular el valor esperado y la varianza de
las variables aleatorias 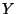 y
y 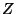 del Problema (4) de la
Guía N
del Problema (4) de la
Guía N 5, usando las funciones densidades allí
obtenidas.
5, usando las funciones densidades allí
obtenidas.
b)Calcular el valor esperado y la varianza de la
variable aleatoria 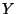 sin usar la función densidad de
sin usar la función densidad de 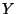 .
.
Problema 3: Suponer que 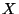 es una variable aleatoria para la cual
es una variable aleatoria para la cual
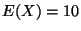 y
y 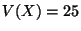 . ¿Para qué valores de las constantes
. ¿Para qué valores de las constantes 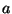 y
y 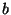 tiene la variable aleatoria
tiene la variable aleatoria 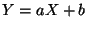 esperanza nula y
varianza
esperanza nula y
varianza 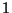 ?
?
Problema 4: Suponer que la variable aleatoria bidimensional 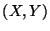 está distribuída uniformemente en el triángulo de la figura:
está distribuída uniformemente en el triángulo de la figura:
a) Obtener las funciones densidad de probabilidad
marginal de 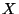 y de
y de 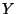 .
.
b) Evaluar 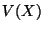 y
y 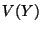 .
.
Problema 5: Suponer que la distribución de probabilidad conjunta de
las variables 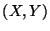 está dada por la siguiente tabla:
donde se cumple que
está dada por la siguiente tabla:
donde se cumple que 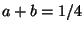 .
.
a) Demostrar que
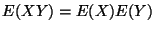 y luego
y luego 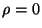 .
.
b) ¿Son las variables 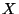 e
e 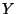 independientes?
independientes?
Problema 6: Supongamos que 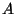 y
y 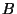 son dos eventos asociados con un
experimento
son dos eventos asociados con un
experimento 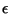 . Supongamos además que
. Supongamos además que 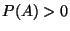 y
y 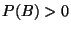 .
Definir las variables aleatorias
.
Definir las variables aleatorias 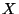 e
e 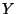 como sigue:
como sigue:
Demostrar que 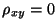 implica que
implica que 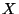 e
e 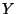 son independientes.
son independientes.
Problema 7: Suponer que la densidad de probabilidad conjunta de 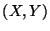 está dada por:
está dada por:
Calcular:
a) Las densidades de probabilidad marginal de 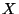 e
e 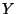 .
.
b) 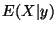 y
y 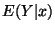 c) Verificar que
c) Verificar que
![$E(X)=E[E(X\vert Y)]$](img31.gif) y
y
![$E(Y)=E[E(Y\vert X)]$](img32.gif)
Problema 8: Dado que 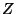 es una variable aleatoria normal estándar,
calcular:
es una variable aleatoria normal estándar,
calcular:
a)
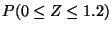
b)
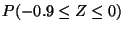
c)
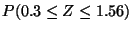
d)
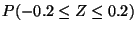
e)
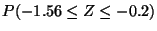
Problema 9: Dado que 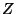 es una variable aleatoria normal estándar,
determinar el valor de
es una variable aleatoria normal estándar,
determinar el valor de 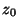 tal que:
tal que:
a)
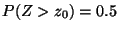
b)
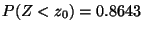
c)
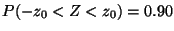
d)
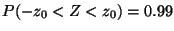
Problema 10: Los promedios de las calificaciones anuales de una gran
población de estudiantes de un colegio tienen una distribución
aproximadamente normal con media igual a 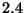 y desviación
estándar igual a
y desviación
estándar igual a 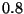 .
.
a) ¿Qué fracción de estudiantes tiene un promedio
superior a 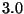 ?
?
b) Si se consideran recursantes a los estudiantes que
tienen promedio igual o inferior a 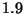 , ¿Qué porcentaje de
estudiantes resultarán recursantes?
, ¿Qué porcentaje de
estudiantes resultarán recursantes?
c) Si el 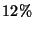 superior de los promedios recibe una
mención especial, ¿Qué promedio mínimo hay que poseer para
conseguir el premio?
superior de los promedios recibe una
mención especial, ¿Qué promedio mínimo hay que poseer para
conseguir el premio?
d) Suponga que se escojen al azar tres estudiantes del
colegio. ¿Cuál es la probabilidad que los tres tengan promedios
superiores a 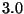 ?
?
Problema 11: Se debe ajustar una máquina para envasar miel de tal manera
que llene en promedio los frascos con 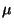 gr por frasco. Si el
proceso de llenado tiene una desviación estándar igual a
gr por frasco. Si el
proceso de llenado tiene una desviación estándar igual a 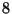 gr,
calcular el valor de
gr,
calcular el valor de 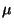 de manera tal que solamente el
de manera tal que solamente el 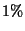 de
los frascos superen los
de
los frascos superen los 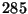 gr de peso.
gr de peso.
Fa.M.A.F ©2002
Pedro Pury
2002-09-27
![\begin{picture}(45.00,55.00)
\put(0.00,10.00){\vector(1,0){45.00}}
\put(5.00,5...
...ebox(0,0)[cl]{$2$}}
\put(27.00,52.00){\makebox(0,0)[cl]{$(2,4)$}}
\end{picture}](img12.gif)