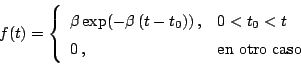Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Guía N 8: Estimación de los Parámetros
8: Estimación de los Parámetros
Problema 1: Una variable aleatoria 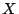 tiene fdp
tiene fdp
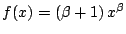 ,
, 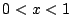 , y
, y 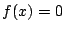 en caso
contrario, siendo
en caso
contrario, siendo 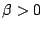 un parámetro desconocido.
un parámetro desconocido.
a) Obtener el estimador de MV (máxima
verosimilitud) de 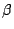 , en base a una muestra
, en base a una muestra
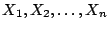 .
.
b) Evaluar el estimador si los valores muestrales son
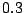 ,
, 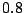 ,
, 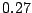 ,
, 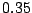 ,
, 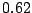 y
y 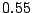 .
.
Problema 2: Suponer que 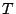 , el tiempo estimado (expresado en horas)
para que ocurra la falla de un instrumento electrónico, tiene
la siguiente fdp:
, el tiempo estimado (expresado en horas)
para que ocurra la falla de un instrumento electrónico, tiene
la siguiente fdp:
siendo 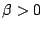 un parámetro desconocido.
un parámetro desconocido.
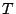 resulta así con una distribución exponencial truncada
a la izquierda de
resulta así con una distribución exponencial truncada
a la izquierda de 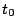 .
Suponer que se prueban
.
Suponer que se prueban 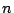 artículos y que se anotan los
tiempos en los cuales estos fallan:
artículos y que se anotan los
tiempos en los cuales estos fallan:
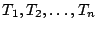 .
.
a) Suponiendo que 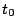 es conocido, obtener el
estimador de MV de
es conocido, obtener el
estimador de MV de 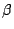 .
.
b) Suponiendo que 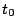 es desconocido, pero
es desconocido, pero 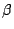 conocida, obtener el estimador de MV de
conocida, obtener el estimador de MV de 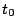 .
.
c) Considerar ahora que se prueban 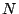 artículos
durante
artículos
durante 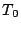 horas (
horas (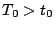 ) y se anota el número
) y se anota el número 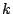 de
artículos que fallan en tal período. Si
de
artículos que fallan en tal período. Si 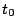 es conocido,
obtener el estimador de MV para
es conocido,
obtener el estimador de MV para 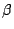 .
.
Problema 3: La variable aleatoria 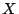 tiene una distribución de
Weibull, cuya densidad de probabilidad, definida para
tiene una distribución de
Weibull, cuya densidad de probabilidad, definida para 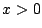 ,
está dada por:
,
está dada por:
Sea
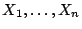 una muestra de la variable aleatoria
una muestra de la variable aleatoria 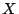 .
Calcular por el método de máxima verosimilitud un estimador
para el parámetro
.
Calcular por el método de máxima verosimilitud un estimador
para el parámetro 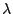 (
(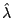 ). Asumir que el
parámetro
). Asumir que el
parámetro 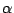 es una constante conocida.
es una constante conocida.
Problema 4: Sea
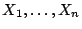 una muestra aleatoria de una variable
con distribución
una muestra aleatoria de una variable
con distribución
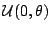 (
(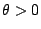 ).
Calcular el estimador de MV para
).
Calcular el estimador de MV para 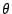 .
¿Es un estimador insesgado?
.
¿Es un estimador insesgado?
Problema 5: La variable 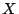 , que mide la resistencia al corte de
soldaduras eléctricas, tiene distribución normal con media
, que mide la resistencia al corte de
soldaduras eléctricas, tiene distribución normal con media
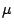 y varianza
y varianza 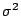 .
Sea
.
Sea
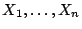 una muestra de la variable aleatoria
una muestra de la variable aleatoria 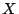 .
.
a) Calcular por el método de máxima verosimilitud
los estimadores para 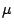 y
y 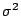 .
.
b) Estimar por máxima verosimilitud el percentil
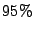 del valor de resistencia al corte; es decir, estimar
del valor de resistencia al corte; es decir, estimar
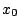 tal que
tal que
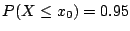 .
.
Problema 6: Comparar el valor de 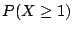 , donde
, donde 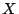 tiene una
distribución
tiene una
distribución 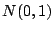 , con
, con 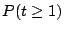 , donde
, donde 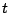 tiene una
distribución
tiene una
distribución 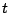 de Student con:
a) 5 g.l., b) 15 g.l. y c) 25 g.l.
de Student con:
a) 5 g.l., b) 15 g.l. y c) 25 g.l.
Problema 7: La variable aleatoria 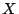 tiene distribución
tiene distribución 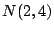 .
Sean
.
Sean
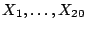 una muestra aleatoria de
una muestra aleatoria de 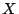 , obtenida
a partir de la Tabla 7 del Apéndice del libro de Paul Meyer.
, obtenida
a partir de la Tabla 7 del Apéndice del libro de Paul Meyer.
a) Suponer que la muestra obtenida corresponde a
una variable aleatoria con distribución
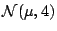 .
Usar los valores muestrales para dar un intervalo de confianza
del
.
Usar los valores muestrales para dar un intervalo de confianza
del 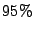 para
para 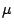 .
.
b) Suponer ahora que la muestra proviene de
una distribución
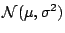 con
con 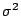 desconocido. Usar nuevamente los valores muestrales para
construir el intervalo de confianza del item anterior.
desconocido. Usar nuevamente los valores muestrales para
construir el intervalo de confianza del item anterior.
c) Comparar las longitudes de los intervalos de
confianza obtenidos en (a) y (b).
d) Suponger que la muestra obtenida corresponde a
una variable aleatoria con distribución
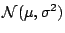 .
Usar los valores muestrales para dar un intervalo de confianza del
.
Usar los valores muestrales para dar un intervalo de confianza del
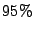 para
para 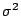 .
.
Problema 8: Suponer que la duración de un componente tiene una
distribución normal, digamos 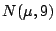 . Se prueban
. Se prueban 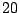 componentes y se anotan los tiempos en los cuales ocurren sus
respectivas fallas
componentes y se anotan los tiempos en los cuales ocurren sus
respectivas fallas
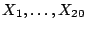 .
Suponer que
.
Suponer que
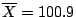 horas.
La confiabilidad de un sistema denotada por
horas.
La confiabilidad de un sistema denotada por 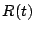 , está
definida según
, está
definida según
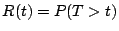 , donde
, donde 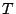 es la variable
correspondiente a la duración del componente hasta su falla.
es la variable
correspondiente a la duración del componente hasta su falla.
a) Obtener un intervalo de confianza bilateral de
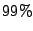 para la confiabilidad
para la confiabilidad 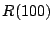 .
.
b) Obtener un intervalo de confianza unilateral
(inferior) de 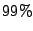 para la confiabilidad
para la confiabilidad 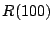 .
.
Problema 9: La siguiente muestra de tamaño 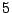 , se obtuvo de la
variable aleatoria bidimensional
, se obtuvo de la
variable aleatoria bidimensional 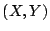 . Usando estos valores,
calcular el coeficiente de correlación muestral.
. Usando estos valores,
calcular el coeficiente de correlación muestral.
Problema 10: Sean 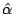 y
y 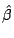 los estimadores de
cuadrados mínimos correspondientes a la relación lineal:
los estimadores de
cuadrados mínimos correspondientes a la relación lineal:
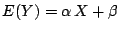 .
.
a) Verificar que estos estimadores son insesgados,
es decir:
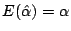 y
y
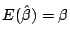 .
.
b) Calcular las varianzas
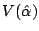 y
y
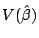 .
.
Problema 11: Suponer que
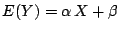 . Se dispone de una
muestra de tamaño
. Se dispone de una
muestra de tamaño 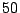 :
: 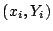 ,
,
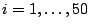 ; para la
cual
; para la
cual
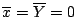 ,
,
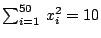 ,
,
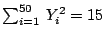 y
y
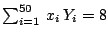 .
.
a) Determinar los estimadores de mínimos cuadrados
de los parámetros 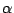 y
y 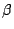 , es decir
, es decir 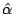 y
y 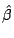 .
.
b) ¿Cuál es el valor de la suma mínima de
cuadrados:
![$\sum_{i=1}^{50} \,[Y_i - (\hat{\alpha} \,x_i + \hat{\beta})]^2$](img69.gif) ?
?
Fa.M.A.F ©2002
Pedro Pury
2002-10-24