Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Probabilidad y Estadística -
Licenciatura en Computación y Profesorados
Guía N 9: Prueba de Hipótesis
9: Prueba de Hipótesis
Problema 1: Suponer que 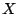 tiene distribución
tiene distribución
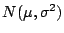 con
con
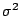 conocida. Para probar
conocida. Para probar
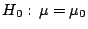 contra
contra
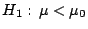 se propone el siguiente método:
Obtener una muestra de tamaño
se propone el siguiente método:
Obtener una muestra de tamaño 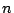 y rechazar
y rechazar 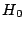 siempre que el
promedio muestral
siempre que el
promedio muestral
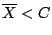 , donde
, donde 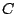 es una constante que
debe determinarse.
es una constante que
debe determinarse.
a) Obtener una expresión para la función de
OC (operación característica), 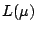 , en términos
de la distribución normal tabulada.
, en términos
de la distribución normal tabulada.
b) Si el nivel de significación de la prueba
es 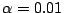 , obtener una expresión para
, obtener una expresión para 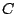 .
.
c) Suponer que 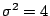 y que se está
probando
y que se está
probando
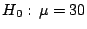 contra
contra
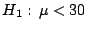 .
Determinar el tamaño de la muestra
.
Determinar el tamaño de la muestra 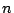 y la constante
y la constante 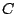 a fin de
satisfacer las condiciones
a fin de
satisfacer las condiciones 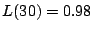 y
y 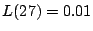 .
.
d) Suponer que se obtienen los siguientes valores
muestrales de 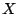 :
:
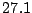
,
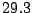
,
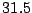
,
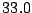
,
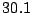
,
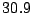
,
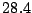
,
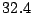
,
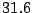
,
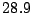
,
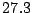
y
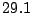
.
¿Rechazaría 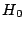 contra
contra 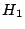 como se estableció en c)
al nivel de significación del
como se estableció en c)
al nivel de significación del 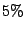 ?
?
Problema 2: Suponer, al igual que en el problema anterior, que 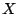 tiene distribución
tiene distribución
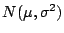 con
con 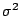 conocida.
Pero ahora, para probar
conocida.
Pero ahora, para probar
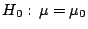 contra
contra
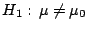 se propone el siguiente método:
Obtener una muestra de tamaño
se propone el siguiente método:
Obtener una muestra de tamaño 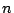 y rechazar
y rechazar 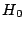 siempre
que
siempre
que
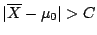 , donde
, donde 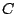 es la constante que
debe determinarse. Bajo estas condiciones responder a los items
a) y b) del problema anterior.
es la constante que
debe determinarse. Bajo estas condiciones responder a los items
a) y b) del problema anterior.
Problema 3: Suponer que 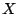 tiene una distribución de Poisson con
parámetro
tiene una distribución de Poisson con
parámetro 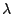 . Para probar
. Para probar
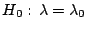 contra
contra
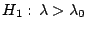 se propone la siguiente
prueba. Obtener una muestra de tamaño
se propone la siguiente
prueba. Obtener una muestra de tamaño 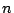 , calcular el
promedio muestral
, calcular el
promedio muestral 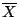 y rechazar
y rechazar 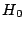 siempre
que
siempre
que
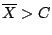 , donde C es una constante que se debe
determinar.
, donde C es una constante que se debe
determinar.
a) Obtener una expresión para la función
de OC, 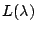 , de la prueba anterior.
, de la prueba anterior.
b) Graficar la función de OC.
c) Suponer que se prueba
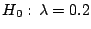 contra
contra
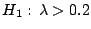 . Se obtiene una muestra de tamaño
. Se obtiene una muestra de tamaño
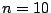 y se rechaza si
y se rechaza si
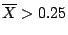 . ¿Cuál es el nivel
de significación de esta prueba?
. ¿Cuál es el nivel
de significación de esta prueba?
Problema 4: De la prueba de varias leyes de falla se ha encontrado que
la distribución exponencial desempeña un papel muy importante.
Por lo tanto, interesa poder decidir si una muestra particular de los
tiempos en los que se presenta una falla, proviene de una
distribución exponencial básica. Suponer que se han probado 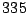 bombillas y que la duración
bombillas y que la duración 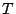 (expresada en horas) está
resumida en la siguiente tabla:
(expresada en horas) está
resumida en la siguiente tabla:
| Duración (horas) |
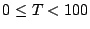 |
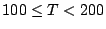 |
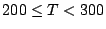 |
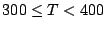 |
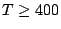 |
N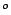 de bombillas de bombillas |
82 |
71 |
68 |
62 |
52 |
De los tiempos registrados para que ocurra la falla, se encontró
que, el promedio muestral
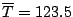 horas.
Utilizando esta información, probar la hipótesis
de que
horas.
Utilizando esta información, probar la hipótesis
de que 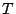 , el tiempo para que ocurra la falla, está
distribuído exponencialmente.
, el tiempo para que ocurra la falla, está
distribuído exponencialmente.
Fa.M.A.F ©2002
Pedro Pury
2002-11-06