Estudio de aspectos fundamentales de la problemática del entrelazamiento de estados cuánticos. Por ejemplo: criterios para detectar separabilidad/entrelazamiento; comportamiento temporal asintótico del entrelazamiento en sistemas abiertos; caracterizacion espectral de estados separables.

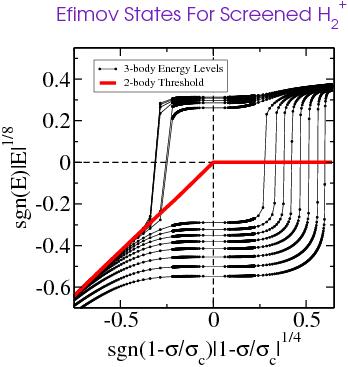
Estudiamos el comportamiento de estados débilmente ligados de sistemas cuánticos de pocos cuerpos en entornos de puntos críticos, donde la energía del estado fundamental cambia abruptamente como función de alguno de los parámetros del Hamiltoniano. Este comportamiento crítico es relevante para estudiar problemas de estabilidad, ionización y/o disociación en Hamiltonianos que modelan átomos o moléculas. Asi proponemos ahora analizar la capacidad de ligar electrones extra en distintos modelos de moléculas, incluyendo potenciales multipolares y moléculas exóticas (donde una o mas de las partículas intervinientes son antipartículas, como positrones o antiprotones).

Otra forma de caracterizar estados cuánticos de sistemas de varias partículas resulta de estudiar el entrelazamiento (entanglement) del mismo. El entrelazamiento de un estado contiene no sólo información acerca de las correlaciones del estado, sino que es de interés en si mismo dado su rol como recurso utilizable en Información Cuántica (IC); manipular el entrelazamiento de un sistema cambiando los parámetros del mismo entonces no solo brinda información sobre la física del problema, sino también sobre su posible utilización para implementar tareas de la IC. El proyecto apunta a estudiar el entrelazamiento en cadenas de spins, trampas de partículas, quantum dots, es decir aquellos sistemas que han sido identificados como posibles escenarios para Ezequiel Farrherla IC. Al mismo tiempo, se pretende estudiar propiedades básicas de estados cuánticos entrelazados como su comportamiento crítico en estados débilmente ligados, su dinámica en sistemas disipativos o su comportamiento en sistemas con interacciones de largo alcance.

Dentro de esta línea de trabajo, nos interesa principalmente el estudio de la "Estructura, Dinámica y Reología de suspensiones coloidales". Los sistemas investigados son las dispersiones coloidales, ya sean, estabilizadas debido a sus cargas eléctricas, con interacciones magnéticas o neutrales (esferas duras).
 Dentro de los métodos empleados para su estudio podemos mencionar: resolución de ecuaciones integro-diferenciales del tipo Orstein-Zernike, para la estructura; y, esquemas de "mode-coupling" para sistemas Brownianos, simulaciones numéricas tipo Dinámica de Stokes y Browiana, para estudiar la dinámica y reología.

Proyectos actuales:

• Difusión y reología de coloides cargados y neutrales.
• Difusión y reología de mezclas coloidales de partículas estabilizadas eléctricamente, y débilmente atractivas.
• Difusión a tiempos largos y reología de suspensiones altamente concentradas de esferas duras.

COLLOIDAL SOFT MATTER

Our research interests are mainly related to the study of the "Structure, Dynamics and Rheology of Colloidal Suspensions". The systems investigated are charge-stabilized, magnetic and neutral colloidal dispersions.
 Within the employed methods, we can mention: Ornstein-Zernike-type integral equation schemes, for the structure; and, mode-coupling schemes for Brownian systems, Stokesian Dynamics and Brownian Dynamics computer simulations, for the dynamics and rheology.

Current projects:

• Diffusion and rheology of charged and neutral colloids.
• Diffusion and rheology in charge-stabilized and weakly attractive colloidal mixtures.
• Long-time self-diffusion and rheology of highly concentrated hard-sphere colloids.

Esta línea se orienta al estudio de las propiedades mecánicas y dinámicas de estructuras supramoleculares cerradas, cuyas paredes están constituidas por membranas. Como ejemplo podemos citar vesículas y liposomas constituidos a base de lípidos. Se estudiarán los mecanismos físicos que determinan la estabilidad de membranas y liposomas, buscando un modelo verificable y consistente que permita relacionar las propiedades mecánicas e hidrodinámicas con las propiedades de estructura y dinámica molecular.

DYNAMICS OF VESICLES AND MEMBRANES

This research line is oriented to the study of the mecanical and dynamical properties of closed supramolecular structures with membrane walls. In particular, lipidic vesicles and liposomes are considered. We study mecanical stability of the vesicles, and its relation to the structure and dynamics of the membrane.