Equilibrio mecánico

Veamos ahora otro ejemplo de equilibrio en nuestro sistema comprendido en la cavidad cilíndrica, ahora con un pistón diatérmico, impermeable a la materia y móvil. El sistema compuesto está aislado del exterior, de modo que $U^{(1)}+U^{(2)}=$ cte, y como el recinto cilíndrico es rígido, $V^{(1)}+V^{(2)}=$ cte. Una vez alcanzado el equilibrio, la entropía debe ser máxima:

$$\begin{eqnarray*} {\rm d}S = \left( \frac{\partial S^{(1)}}{\partial U^{(1)}}... ...ial V^{(2)}} \right)_{U^{(2)},\{n_j^{(2)}\}} {\rm d}V^{(2)} =0 \end{eqnarray*}$$

Nuevamente, teniendo en cuenta que ${\rm d}U^{(2)}=- {\rm d}U^{(1)}$ y también que ${\rm d}V^{(2)}=- {\rm d}V^{(1)}$,

$${\rm d}S = \left(\frac{1}{T^{(1)}}-\frac{1}{T^{(2)}}\righ... ...)}}{T^{(1)}}-\frac{P^{(2)}}{T^{(2)}}\right) {\rm d}V^{(1)}=0$$

Como esta expresión debe anularse para ${\rm d}U^{(1)}$ y ${\rm d}V^{(1)}$ arbitrarios, debe cumplirse

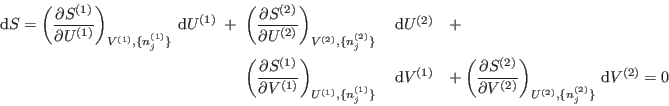
$T^{(1)} =T^{(2)}\rule[-1.6em]{0em}{4em}$         y          $P^{(1)} =P^{(2)}\rule[-1.6em]{0em}{4em}$

Nuevamente, ambos resultados coinciden con lo esperado ``intuitivamente''. Como en el ejemplo anterior, las ecuaciones logradas permiten obtener la solución formal para el problema, es decir, los valores finales para $U^{(1)},V^{(1)},\{n_j^{(1)}\},U^{(2)},V^{(2)},\{n_j^{(2)}\}$ ( ${n_j^{(\alpha)}}$ son constantes).