Un gas ideal simple está descripto por las ecuaciones
donde 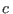 es una constante característica del tipo de gas y se involucra a
la constante universal de los gases
es una constante característica del tipo de gas y se involucra a
la constante universal de los gases
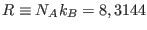 J/(mol K),
siendo
J/(mol K),
siendo 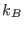 la constante de Boltzmann. Los gases monoatómicos cuyos átomos
se pueden decribir como masas puntuales que no interactúan entre sí se
comportan siguiendo estas relaciones para temperaturas altas (
la constante de Boltzmann. Los gases monoatómicos cuyos átomos
se pueden decribir como masas puntuales que no interactúan entre sí se
comportan siguiendo estas relaciones para temperaturas altas (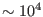 K)
y presiones relativamente bajas, valiendo en estos casos
K)
y presiones relativamente bajas, valiendo en estos casos 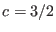 . Hay otros
gases reales que bajo ciertas condiciones también satisfacen las ecuaciones
anteriores con otros valores para
. Hay otros
gases reales que bajo ciertas condiciones también satisfacen las ecuaciones
anteriores con otros valores para 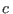 (5/2, 7/2, etc.).
(5/2, 7/2, etc.).
A partir de las ecuaciones anteriores puede arribarse a la ecuación
fundamental. Como en esas ecuaciones de estado aparece 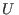 explícitamente,
resulta natural elegir la representación entropía. Reescribimos las
ecuaciones anteriores en la forma
explícitamente,
resulta natural elegir la representación entropía. Reescribimos las
ecuaciones anteriores en la forma
Utilizando la relación de Gibbs-Duhem puede obtenerse 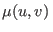 a partir de
estas ecuaciones de estado
a partir de
estas ecuaciones de estado
Reemplazando
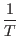 y
y
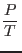 en términos de
en términos de
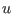 y
y 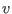 , reescribimos
, reescribimos
Mediante integración directa se obtiene
donde el subíndice  señala un estado de referencia. De este modo,
estamos en condiciones de escribir la ecuación fundamental usando la
relación de Euler
señala un estado de referencia. De este modo,
estamos en condiciones de escribir la ecuación fundamental usando la
relación de Euler
es decir
o bien
donde se ha definido
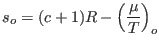 .
.
Por supuesto, para llegar a la ecuación fundamental hay varias vías
alternativas a la que se eligió aquí. En particular, se puede partir de la
forma diferencial para la entropía molar
que también se integra directamente para obtener
equivalente a la expresión anterior.
En realidad no siempre es posible arribar a ecuaciones diferenciales en las
que puedan separarse tan fácilmente las variables. En general, esta
limitación es importante y usualmente debe acudirse a otras herramientas.
Gustavo Castellano 12/06/2018
![]() explícitamente,
resulta natural elegir la representación entropía. Reescribimos las
ecuaciones anteriores en la forma
explícitamente,
resulta natural elegir la representación entropía. Reescribimos las
ecuaciones anteriores en la forma
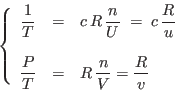
![\begin{displaymath}
\fbox{ $S(U,V,n) = n s_o + nR \ln \left[ \displaystyl...
..._o}n\right)^{c+1} \right]\;, \rule[-1.75em]{0em}{4em} $ }
\end{displaymath}](img200.png)