Condiciones de estabilidad para los potenciales termodinámicos

Para hallar las condiciones de estabilidad que debe cumplir la energía interna, simplemente hay que transcribir con cuidado el desarrollo anterior, utilizando el principio de energía mínima en lugar del principio de entropía máxima. De esta manera arribamos a conclusiones similares, pero donde aparece la condición de concavidad para la representación entropía, en la representación energía esto debe traducirse como convexidad; es decir

$$U(S+\Delta S,X+\Delta X,n) + U(S-\Delta S,X-\Delta X,n) \; \geq \; 2\; U(S,X,n) \qquad \forall \Delta S,\Delta X \;,$$

Cuando $\Delta S,\Delta X \to 0$, esta condición se traduce como

$$\left(\frac{\partial^2 U}{\partial S^2}\right)_{X,n} \le... ...(\frac{\partial T}{\partial S}\right)_{X,n} \right] \geq 0 \;;$$

$$\left(\frac{\partial^2 U}{\partial X^2}\right)_{S,n} \le... ...eft(\frac{\partial Y}{\partial X}\right)_{S,n} \right] \geq 0$$

y

$$\frac{\partial²U}{\partial S²} \frac{\partial²U}{\partial... ...rac{\partial^2U\/}{\partial S \partial X}\right)^2 \geq 0 \;.$$

La primera de estas condiciones implica que las capacidades caloríficas molares $c_X$ son siempre positivas; la segunda impone que, en el caso de un gas, la compresibilidad adiabática $\kappa_S$ es también positiva. En la próxima sección discutiremos estos resultados más detalladamente.

Estas condiciones pueden trasladarse fácilmente a cualquier transformada de Legendre de la energía interna. Para ello debemos lograr ver qué ocurre con una concavidad de $U$ al efectuar una transformada de Legendre. Se deja como ejercicio al lector demostrar que, partiendo de que $U$ es convexa en la variable extensiva $X_j (j=0,1,\dots;X_j=S,X,\dots,\{n_k\})$, la transformada $\psi_j=U-Y_jX_j$ es cóncava en la variable $Y_j\equiv\partial U/\partial X_j$ (la convexidad en las variables no transformadas se mantiene).

A partir de las condiciones de estabilidad para $U$, esta propiedad se traduce como

$$\begin{eqnarray*} \star\quad \left(\frac{\partial^2 F}{\partial T^2}\right)_{X... ...uad \left(\frac{\partial^2 G}{\partial Y^2}\right)_{T,n} \leq 0 \end{eqnarray*}$$

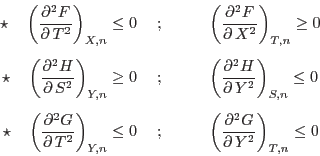
Sólo para completar con una ilustración, analicemos el caso del potencial de Helmholtz para un fluido en función del volumen. La gráfica entonces corresponde a una isoterma, y la condición de estabilidad elimina el tramo comprendido entre $A$ y $D$, reemplazándolo por el segmento recto que se ha dibujado. En esta representación es evidente que los estados $A$ y $D$ comparten no sólo $T$ y $n$, sino además $P\equiv-(\partial F/\partial V)_{T,n}$, de modo que es fácil pensar que dos sistemas en estos estados coexisten en el equilibrio, y el segmento recto permite mezclar partes de esos estados para solucionar el problema de la inestabilidad. Un sistema homogéneo elige entonces distribuirse, una parte en el estado $A$ y otra en el estado $D$, ya que de ese modo se satisface el principio de mínimo para el potencial de Helmholtz.

 

En este ejemplo vale la pena verificar que si bien los estados comprendidos entre $B$ y $C$ quedan excluidos debido a que no satisfacen el criterio de estabilidad local, los tramos $AB$ y $CD$ corresponden a las regiones que reconocíamos en las isotermas de los diagramas $P$-$V$ para los fluidos de Van der Waals, y representan estados de equilibrio metaestable.