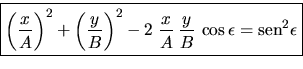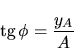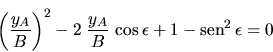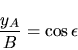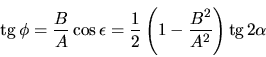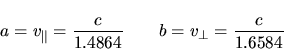Ecuación en el sitema primado:
Ecuación en el sistema no primado:
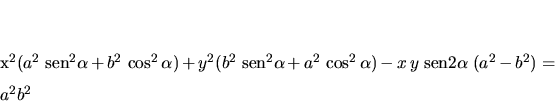 |
(1) |
 Valor extremo de y: B
Valor extremo de y: B
 Valor extremo de x: A
Valor extremo de x: A
Cálculos auxiliares:
Resulta entonces:
Substituyendo en (1):
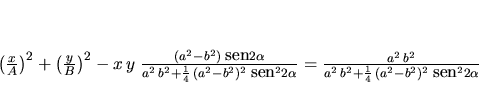 |
(2) |
Definiendo:
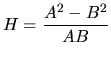 :
:
Entonces definiendo:
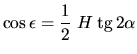 ,
resulta que la ecuación (2) puede escribirse según:
,
resulta que la ecuación (2) puede escribirse según:
Nota: Ver Polarización Elíptica en:
Hecht, Optics, Chap.8.
Aplicación:
Propagación del rayo
extraordinario en una placa plano-paralela de calcita
Una sección principal de un cristal de calcita contine el eje
óptico, el cual forma con la cara de incidencia un ángulo
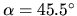 . Bajo incidencia normal sobre el cristal,
el rayo ordinario (cuya polarización es normal a la sección
principal) no se refracta, mientras que el rayo extraordinario
(cuya polarización está sobre la sección principal) encuentra
un medio inhomogéneo para el cual la velocidad de propagación a
lo largo del eje óptico (
. Bajo incidencia normal sobre el cristal,
el rayo ordinario (cuya polarización es normal a la sección
principal) no se refracta, mientras que el rayo extraordinario
(cuya polarización está sobre la sección principal) encuentra
un medio inhomogéneo para el cual la velocidad de propagación a
lo largo del eje óptico (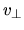 ) es menor que la velocidad en
la dirección perpendicular al eje (
) es menor que la velocidad en
la dirección perpendicular al eje (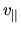 ).
La dirección resultante para el rayo extraordinario forma un
ángulo
).
La dirección resultante para el rayo extraordinario forma un
ángulo 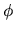 con la normal a la cara, tal que se cumple:
con la normal a la cara, tal que se cumple:
Tomando 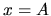 en la ecuación de la elipse:
en la ecuación de la elipse:
De lo cual resulta:
y por lo tanto:
Sustituyendo según:
resulta finalmente:
Pedro Pury
2001-02-14


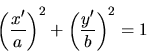

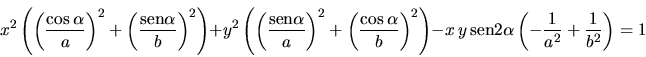
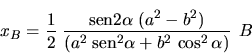
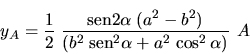
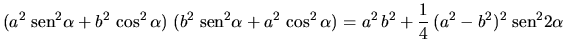
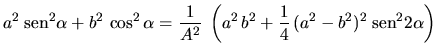
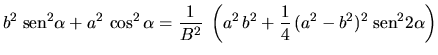
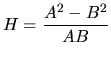 :
:
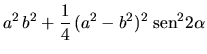
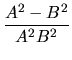
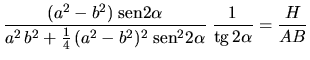
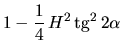
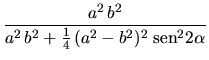
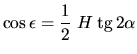 ,
resulta que la ecuación (2) puede escribirse según:
,
resulta que la ecuación (2) puede escribirse según: