

Next: Estimación del error de
Up: La simulación de Buffon
Previous: Introducción
Tarea: Escribir un programa que simule en la
computadora la técnica mencionada de arrojar la aguja. Esto
resulta mucho más cómodo que efectivamente dejar caer una
aguja sobre una hoja rayada. Notar que el problema es equivalente
a sortear uniformente la posición del centro de la aguja en un
intervalo de ancho 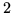 , y sortear el ángulo que forma la aguja de
largo
, y sortear el ángulo que forma la aguja de
largo 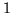 con la dirección de la recta que contiene al intervalo
de interés, uniformemente entre
con la dirección de la recta que contiene al intervalo
de interés, uniformemente entre 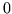 y
y 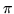 . Para cada prueba
verificar a continuación si la proyección de la aguja sobre
la recta mencionada, interseca algún extremo del intervalo.
. Para cada prueba
verificar a continuación si la proyección de la aguja sobre
la recta mencionada, interseca algún extremo del intervalo.
Las variables que se sortean uniformemente son: ![$r \in [0,2]$](img5.gif) y
y
![$\theta \in [0, \pi]$](img6.gif) [1]. En consecuencia las ordenadas
de los extremos de la aguja resultan:
[1]. En consecuencia las ordenadas
de los extremos de la aguja resultan:
Se considera que se produce intersección si
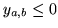 ó
ó
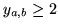 . Claramente, no existirá intersección si
. Claramente, no existirá intersección si
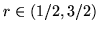 . En la siguiente tabla se registra los resultados de una
simulación realizada en FORTRAN. En la primer columna registra el
número de veces que se sorteó la posición de la aguja y la
segunda columna registra la inversa de la frecuencia con la que los
extremos de aguja salen del intervado de ancho
. En la siguiente tabla se registra los resultados de una
simulación realizada en FORTRAN. En la primer columna registra el
número de veces que se sorteó la posición de la aguja y la
segunda columna registra la inversa de la frecuencia con la que los
extremos de aguja salen del intervado de ancho 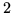 .
.
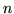 |
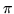 |
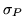 |
| 1.000 |
3.0120482 |
0.15 |
| 10.000 |
3.1113877 |
0.046 |
| 100.000 |
3.1401118 |
0.015 |
| 1.000.000 |
3.1462569 |
0.0046 |
| 10.000.000 |
3.1408347 |
0.0015 |
| 100.000.000 |
3.1425390 |
0.00046 |
| 1.000.000.000 |
3.1418059 |
0.00015 |
Nota: Para realizar la simulación el programa
utiliza el valor de 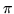 que quiere estimarse. Esto sin
embargo, no constituye un fraude dado que sólo se lo utiliza
para simular el proceso de arrojar la aguja, no en el cálculo
del número en sí.
que quiere estimarse. Esto sin
embargo, no constituye un fraude dado que sólo se lo utiliza
para simular el proceso de arrojar la aguja, no en el cálculo
del número en sí.


Next: Estimación del error de
Up: La simulación de Buffon
Previous: Introducción
Pedro Pury
2001-10-04