

Next: Justificación teórica de la
Up: La simulación de Buffon
Previous: Simulación en Computadora
Tarea: Estimar el valor de 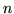 (número de
pruebas) necesario para asegurar el valor de
(número de
pruebas) necesario para asegurar el valor de 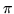 con cinco
cifras significativas (es decir que el error afecte recién al
sexto decimal).
con cinco
cifras significativas (es decir que el error afecte recién al
sexto decimal).
El estimador insesgado de la frecuencia con la cual la aguja corta
los renglones es 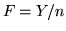 , donde
, donde 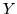 es el número de veces que se
produce intersección al realizar
es el número de veces que se
produce intersección al realizar 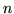 pruebas al azar. Resulta:
pruebas al azar. Resulta:
De esta forma el estimador de 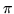 es la variable aleatoria
es la variable aleatoria 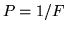 .
En general para una variable
.
En general para una variable 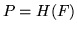 , conociendo
, conociendo 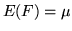 y
y
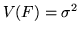 , se pueden utilizar las fórmulas aproximadas
, se pueden utilizar las fórmulas aproximadas
Resulta entonces
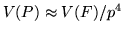 y en consecuencia
y en consecuencia
En la última columna de la tabla anterior se consignan los valores
de 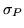 correspondientes a cada valor de
correspondientes a cada valor de 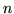 .
En particular si se desea
.
En particular si se desea
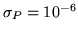 resulta
resulta
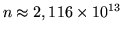 .
.
Pedro Pury
2001-10-04