

Next: Bibliography
Up: La simulación de Buffon
Previous: Estimación del error de
Tarea: En base a la Teoría de la Probabilidad
elaborar un argumento que explique porqué el método de arrojar la
aguja funciona para estimar el valor de 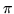 .
.
En la siguiente figura se representa la situación en la cual la
aguja presenta el máximo ángulo (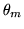 ) posible para que
exista intersección, dada una distancia
) posible para que
exista intersección, dada una distancia 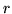 desde el centro de la
aguja al renglón.
Tenemos entonces la relación
desde el centro de la
aguja al renglón.
Tenemos entonces la relación
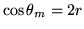 (
(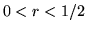 ).
El area encerrada bajo la curva definida por la función
).
El area encerrada bajo la curva definida por la función
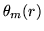 resulta entonces:
resulta entonces:
Tenemos entonces que en el plano 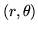 se sortean
uniformemente los puntos del rectángulo descripto en la siguiente
figura cuya area es
se sortean
uniformemente los puntos del rectángulo descripto en la siguiente
figura cuya area es 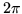 . Por otro lado las areas encerradas
por las curvas de ángulo máximo y las verticales en
. Por otro lado las areas encerradas
por las curvas de ángulo máximo y las verticales en 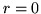 y
y
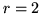 , y que corresponden a las situaciones de intersección, suman
, y que corresponden a las situaciones de intersección, suman
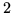 . Por lo tanto la probabilidad de intersección resulta
. Por lo tanto la probabilidad de intersección resulta 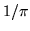 .
.


Next: Bibliography
Up: La simulación de Buffon
Previous: Estimación del error de
Pedro Pury
2001-10-04
![\begin{picture}(40.00,20.00)
\put(0.00,20.00){\line(1,0){40.00}}
\put(20.00,10...
...{$\theta_m$}}
\put(28.00,13.00){\makebox(0,0)[cc]{$\frac{1}{2}$}}
\end{picture}](img28.gif)
![\begin{picture}(40.00,20.00)
\put(0.00,20.00){\line(1,0){40.00}}
\put(20.00,10...
...{$\theta_m$}}
\put(28.00,13.00){\makebox(0,0)[cc]{$\frac{1}{2}$}}
\end{picture}](img28.gif)
![\begin{picture}(45.00,47.00)
\put(5.00,5.00){\vector(1,0){40.00}}
\put(5.00,5....
...9.33,47.00){\makebox(0,0)[cc]{$\theta_{m} = \mbox{arc} \cos 2 r$}}
\end{picture}](img32.gif)
![\begin{picture}(55.00,40.00)
\put(5.00,20.00){\vector(1,0){50.00}}
\put(5.00,0...
...,0)[cc]{$\frac{1}{2}$}}
\put(47.67,17.33){\makebox(0,0)[cc]{$2$}}
\end{picture}](img40.gif)