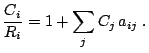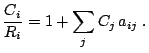Siguiente: Claisse-Quintin.
Subir: Método de Rousseau
Anterior: Método de Rousseau
Estos autores propusieron en 1966 la siguiente
expresión para la corrección por efectos de matriz:
Esta expresión coincide con la (3) si
Notemos que los coeficientes contienen todos los efectos de
matriz (absorción y reforzamiento) juntos. Lachance y Traill originalmente
tomaban
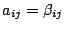 , una aproximación válida si no hay reforzamiento
y si además el haz policromático incidente se reemplaza por uno
monocromático con cierto valor promedio de energía.
, una aproximación válida si no hay reforzamiento
y si además el haz policromático incidente se reemplaza por uno
monocromático con cierto valor promedio de energía.
Gustavo Castellano 15/05/2009