Siguiente: Lachance-Traill.
Subir: Análisis cuantitativo
Anterior: Análisis cuantitativo
Los parámetros geométricos y atómicos que figuran en la expresión
(1) son muy difíciles de determinar, por lo que habitualmente se
recurre a un estándar de composición conocida, de modo que al realizar el
cociente todos estos factores se cancelan. Teniendo presente esto, para el
caso de una muestra ``semiinfinita'' reescribimos
donde hemos elegido notar
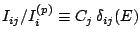 . Si
se tiene el espectro incidente como un vector de intensidades
. Si
se tiene el espectro incidente como un vector de intensidades
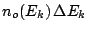 correspondientes a energías en el intervalo
correspondientes a energías en el intervalo
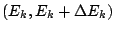 y se define
y se define
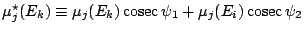 , el
denominador de la expresión anterior puede reemplazarse por
, el
denominador de la expresión anterior puede reemplazarse por
donde se ve, de la última definición, que
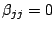 . Resulta oportuno
aquí introducir el parámetro
. Resulta oportuno
aquí introducir el parámetro
de modo que si se compara con un patrón puro, tendremos
La razón de intensidades resulta entonces
de donde
El factor que acompaña a 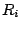 en el miembro de la derecha se denomina
`corrección por efectos de matriz', y al escribirlo de esta manera
distinguimos las correcciones por absorción en el numerador, que
tienen en cuenta las diferencias entre la atenuación de la radiación
en el miembro de la derecha se denomina
`corrección por efectos de matriz', y al escribirlo de esta manera
distinguimos las correcciones por absorción en el numerador, que
tienen en cuenta las diferencias entre la atenuación de la radiación 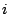 por el elemento
por el elemento 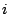 y por el elemento
y por el elemento 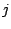 , mientras que en el denominador
se corrige por reforzamiento. Aunque este último siempre es mayor o
igual que 1, en el numerador el valor de
, mientras que en el denominador
se corrige por reforzamiento. Aunque este último siempre es mayor o
igual que 1, en el numerador el valor de
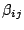 puede ser negativo,
por lo que la corrección por absorción puede ser mayor o menor que 1.
puede ser negativo,
por lo que la corrección por absorción puede ser mayor o menor que 1.
Podemos reescribir (una vez más) la expresión anterior como
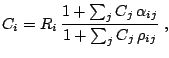 |
(3) |
donde definimos los coeficientes de influencia o interacción
binaria
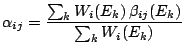
y
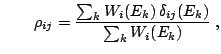
que pueden interpretarse como promedios pesados de las contribuciones para
cada 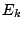 . Claramente,
. Claramente,
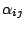 y
y
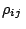 cambian con la
composición de la muestra (
cambian con la
composición de la muestra (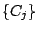 ), de manera que no dependen sólo de los
elementos
), de manera que no dependen sólo de los
elementos 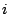 y
y 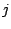 , y por consiguiente no pueden evaluarse por separado
las contribuciones correspondientes a cada
, y por consiguiente no pueden evaluarse por separado
las contribuciones correspondientes a cada 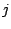 .
.
A continuación analizaremos tres de los llamados ``métodos empíricos'',
intentando encontrar una conexión entre ellos y el método de parámetros
fundamentales (3).
Subsecciones



Siguiente: Lachance-Traill.
Subir: Análisis cuantitativo
Anterior: Análisis cuantitativo
Gustavo Castellano 15/05/2009
![$\displaystyle I_i = G_i C_i \int_{E_c}^{E_{\mbox{\tiny máx}}}\!\! {\rm d}E ...
...\psi_1 + \mu(E_i)\cosec\psi_2}
\left[ 1+\sum_j C_j \delta_{ij}(E) \right] \;,
$](img57.png)
![$\displaystyle I_i = G_i C_i \int_{E_c}^{E_{\mbox{\tiny máx}}}\!\! {\rm d}E ...
...\psi_1 + \mu(E_i)\cosec\psi_2}
\left[ 1+\sum_j C_j \delta_{ij}(E) \right] \;,
$](img57.png)
![\begin{displaymath}
\begin{split}
\sum_j C_j \mu_j^\star(E_k) & = C_i \mu_i^\...
...k) \left[ 1+\sum_j C_j \beta_{ij}(E_k) \right] \;,
\end{split}\end{displaymath}](img62.png)
![$\displaystyle W_i(E_k) \equiv \frac{\tau_i(E_k) n_o(E_k) \Delta E_k}
{\mu_i^\star(E_k) \left[ 1+\sum_j C_j \beta_{ij}(E_k) \right]} \;,
$](img64.png)
![$\displaystyle I_i^o = G_i\sum_k\frac{\tau_i(E_k) n_o(E_k) \Delta E_k}{\mu_i^\star(E_k)}
= G_i \sum_k W_i(E_k)\left[ 1+\sum_j C_j \beta_{ij}(E_k) \right] \;.
$](img65.png)
![$\displaystyle R_i = \frac{C_i \sum_k W_i(E_k)\left[ 1+\sum_j C_j \delta_{ij}(E_k) \right]}
{\sum_k W_i(E_k)\left[ 1+\sum_j C_j \beta_{ij}(E_k) \right]} \;,
$](img66.png)
![$\displaystyle C_i = R_i \frac{\sum_k W_i(E_k)\left[ 1+\sum_j C_j \beta_{ij}(E_k) \right]}
{\sum_k W_i(E_k)\left[ 1+\sum_j C_j \delta_{ij}(E_k) \right]} \;.
$](img67.png)
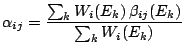 y
y