|
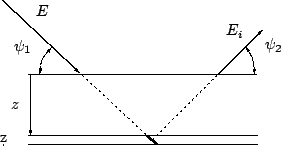
La predicción de intensidades características que llegan al detector en un
experimento de XRF ha sido desarrollada por Sherman en 1955, y es también
conocida como parámetros fundamentales. Si el haz con que se
irradia el material que se desea analizar tiene una intensidad
|
|
de fotones
característicos primarios para la línea de interés del elemento
![]() provenientes de una capa de espesor diferencial
provenientes de una capa de espesor diferencial
![]() a una
profundidad
a una
profundidad ![]() es
es
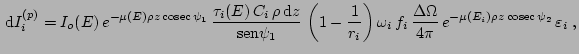
donde
Si se desea incluir el espectro policromático de un tubo de rayos x, debe
sustituirse ![]() por infinitos ``sumandos''
por infinitos ``sumandos''
![]() , y la expresión se completa integrando para todo el rango de
energías involucrado en el espectro del tubo.
, y la expresión se completa integrando para todo el rango de
energías involucrado en el espectro del tubo.
En el caso particular de muestras infinitas, el numerador del último factor
se hace 1, simplificando un poco la expresión. Por otro lado, si se trata de
muestras delgadas, todo el último factor se vuelve ![]() y entonces sí
puede obtenerse una expresión para
y entonces sí
puede obtenerse una expresión para ![]() como función de la intensidad
registrada, y por supuesto de todos los parámetros atómicos y
experimentales. De todos modos, muchos de esos parámetros son imposibles de
conocer, lo que hace que habitualmente se normalicen las intensidades con
determinaciones idénticas en un patrón de composición conocida
como función de la intensidad
registrada, y por supuesto de todos los parámetros atómicos y
experimentales. De todos modos, muchos de esos parámetros son imposibles de
conocer, lo que hace que habitualmente se normalicen las intensidades con
determinaciones idénticas en un patrón de composición conocida ![]() ,
obteniendo así la última expresión de la sección anterior.
,
obteniendo así la última expresión de la sección anterior.
En la expresión (1) no se ha tenido en cuenta el
reforzamiento de otros fotones característicos ![]() , que al tener
energía suficiente podrían ionizar a su vez el elemento de interés,
provocando un aumento
, que al tener
energía suficiente podrían ionizar a su vez el elemento de interés,
provocando un aumento ![]() en la intensidad detectada. En principio,
éste es un efecto de segundo orden, pero cuando el elemento de interés
en la intensidad detectada. En principio,
éste es un efecto de segundo orden, pero cuando el elemento de interés
![]() se encuentra en concentraciones muy bajas y el elemento
se encuentra en concentraciones muy bajas y el elemento ![]() es
mayoritario, las correspondientes correcciones pueden ser muy importantes.
La expresión anterior debe corregirse mediante un factor global
es
mayoritario, las correspondientes correcciones pueden ser muy importantes.
La expresión anterior debe corregirse mediante un factor global
![]() , donde la suma debe abarcar todos los elementos de la
muestra capaces de reforzar al elemento
, donde la suma debe abarcar todos los elementos de la
muestra capaces de reforzar al elemento ![]() . Se deja como ejercicio
verificar que en el caso de radiación monocromática y espesores infinitos,
cada sumando del reforzamiento se escribe como
. Se deja como ejercicio
verificar que en el caso de radiación monocromática y espesores infinitos,
cada sumando del reforzamiento se escribe como
![\begin{displaymath}\begin{split}\frac{I_{ij}}{I_i^{(p)}} = \frac12 &\tau_j(E) ...
...c{\mu(E_i)\cosec\psi_2}{\mu(E_j)}\right) \right]\;. \end{split}\end{displaymath}](img55.png) |
(2) |