


Siguiente: Curvas de calibración
Subir: Método de Rousseau
Anterior: Claisse-Quintin.
En 1974 estos autores propusieron
que coincide con la (3) cuando
y además
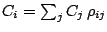 , lo que no siempre es cierto. En
particular Rasberry y Heinrich afirmaban que cuando hay reforzamiento
, lo que no siempre es cierto. En
particular Rasberry y Heinrich afirmaban que cuando hay reforzamiento
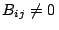 y
y 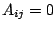 , lo cual es falso.
, lo cual es falso.
Cuando no hay reforzamiento,
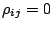 , y la expresión de Lachance y
Traill coincide con la de Claisse y Quintin.
, y la expresión de Lachance y
Traill coincide con la de Claisse y Quintin.
Gustavo Castellano 15/05/2009
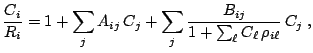
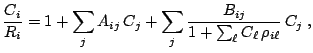
![]() , y la expresión de Lachance y
Traill coincide con la de Claisse y Quintin.
, y la expresión de Lachance y
Traill coincide con la de Claisse y Quintin.