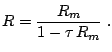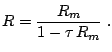Siguiente: Corrección por efectos de
Subir: Errores sistemáticos
Anterior: Errores sistemáticos
Los sistemas de detección siempre requieren de cierto tiempo para poder
procesar la señal generada por los fotones registrados. Éste se denomina
tiempo muerto 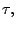 y representa el lapso durante el cual
el sistema se bloquea cada vez que arriba un fotón. Si bien este tiempo
muerto es pequeño, la inactividad a que se refiere hace que el número de
cuentas registrado por unidad de tiempo
y representa el lapso durante el cual
el sistema se bloquea cada vez que arriba un fotón. Si bien este tiempo
muerto es pequeño, la inactividad a que se refiere hace que el número de
cuentas registrado por unidad de tiempo 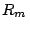 sea menor que el número de
fotones
sea menor que el número de
fotones 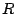 que realmente llega al detector. Se deja como ejercicio
deducir que estas cantidades están relacionados según
que realmente llega al detector. Se deja como ejercicio
deducir que estas cantidades están relacionados según
El tiempo muerto es suficientemente pequeño como para que en general
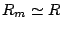 , aunque para tasas de conteo suficientemente altas esta
corrección se vuelve importante (no es válida la expresión anterior) y no
se la puede ignorar si se desea caracterizar seriamente una muestra. En
particular, en sistemas dispersivos en longitudes de onda la corrección por
tiempo muerto puede variar de una línea a otra, e incluso dentro del
intervalo angular correspondiente a un único pico, con lo cual la
distorsión de los resultados puede volverse exagerada.
, aunque para tasas de conteo suficientemente altas esta
corrección se vuelve importante (no es válida la expresión anterior) y no
se la puede ignorar si se desea caracterizar seriamente una muestra. En
particular, en sistemas dispersivos en longitudes de onda la corrección por
tiempo muerto puede variar de una línea a otra, e incluso dentro del
intervalo angular correspondiente a un único pico, con lo cual la
distorsión de los resultados puede volverse exagerada.



Siguiente: Corrección por efectos de
Subir: Errores sistemáticos
Anterior: Errores sistemáticos
Gustavo Castellano 15/05/2009