Espectrómetros dispersivos en longitudes de onda

La configuración más sencilla es la de un cristal plano cuya separación interplanar es , que difracta el haz de fotones hacia un contador de rayos x registrando las longitudes de onda $\lambda$ de acuerdo a la ley de Bragg $n \lambda=2 d {\rm sen}\theta$ , donde es un número entero y $\theta$ , el llamado ángulo de Bragg. Rotando el cristal y el contador (el doble de rápido) se puede barrer cierto rango de valores para $\theta$ , registrando el espectro de interés.

Está claro que además del primer orden ( ) pueden aparecer órdenes superiores en determinado ángulo; un rudimentario análisis de altura de pulsos es suficiente para eliminar este efecto indeseado, descartándose las longitudes de onda correspondientes a . Para el rango de $\lambda$ queda determinado por la separación interplanar .

En los últimos años se han logrado valores de notablemente mayores a los tradicionales, destacándose los multicapas, construidos depositando alternadamente capas de elementos (o compuestos) livianos y pesados. Con estos últimos es posible la detección de los elementos más livianos. Algunos valores de para diferentes cristales se muestran en la tabla de la derecha.

$\begin{center}\vbox{\input{bragg.epic} }\end{center}$

Material		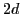(Å)
Fluoruro de litio	LiF	4,02
Cuarzo		6,69
Pentaerytritol	PET	8,74
Fosfato dihidrógeno de amonio	AdP	10,64
Mica		19,84
Ftalato ácido de talio	TAP	39
Laurato de plomo		70
Estearato decanoato de plomo		100
Melisato de plomo		160

Una característica distintiva de los sistemas dispersivos en longitudes de onda es su alta resolución, relacionada con la tolerancia con la que se registra la radiación que satisface la condición de Bragg. Como contrapartida, las intensidades que se miden suelen ser bajas: en una microsonda en particular, el área de los emisores (materiales irradiados) suele ser pequeña, por lo que la condición de Bragg se cumple en una superficie muy reducida del cristal. Para mejorar la eficiencia en la detección se utilizan cristales curvos que de alguna manera focalizan el haz refractado.

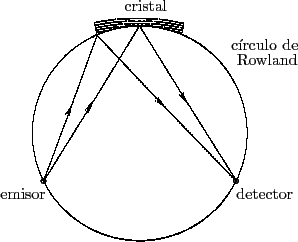
La disposición geométrica ideal debería contener al emisor (muestra), el cristal y el detector en una circunferencia de radio 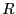, conocida como círculo de Rowland; el radio de curvatura de los planos cristalinos debe ser 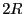, aunque su superficie debe estar pulida de modo que todos sus puntos pertenezcan a la circunferencia de radio 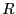. Se deja como ejercicio mostrar que con este diseño, conocido como geometría Johansson (1932), cuando se cumple la condición de Bragg, se cumple para todas las reflexiones que se dan en el cristal.

Por supuesto, los fotones que no viajan en el plano del círculo de Rowland no cumplen con la

$\begin{center}\vbox{\input{johansso.epic} }\end{center}$

condición de Bragg, por lo que se han realizado intentos de cristales con `doble curvatura'; esta alternativa ha sido poco utilizada, pues el otro radio correspondiente a la curvatura perpendicular al plano mencionado dependería de la longitud de onda analizada.

Usualmente el cristal está curvado como en el esquema anterior, aunque su pulido suele ser muy difícil de realizar. Se utiliza esta configuración sin pulir, y se la conoce como geometría Johan (1931), sacrificando un poco la resolución, aunque ganando en intensidad. Si bien se pierde la condición de Bragg cuando la reflexión se aparta del centro, suelen utilizarse colimadores cuyas dimensiones se fijan para optimizar las mediciones.

La elección de la curvatura del círculo de Rowland depende de cuánto puede deformarse el cristal analizador, cuánto puede acercárselo a la muestra, y también por la necesidad de tener el recinto en vacío ( 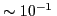$\sim10^{-1}$ torr) a un tamaño conveniente. Esta imposición está relacionada con la búsqueda de la mejor resolución posible. Los valores típicos que se tienen para 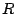rondan los 10cm - 25cm.

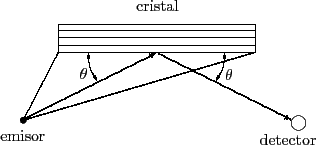
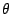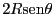Habitualmente se desea mantener constante el ángulo de salida de la radiación (take-off): para ello el cristal se mueve a lo largo de una recta que pasa por el emisor y también rota para conseguir el ángulo $\theta$ correspondiente a la condición de Bragg, de modo que la distancia al emisor vale $2R{\rm sen}\theta$ . El contador gaseoso se mueve consecuentemente para permanecer siempre en el círculo de Rowland.

Los equipos modernos poseen varios cristales montados en sus respectivos espectrómetros, lo que permite lograr análisis multielemental en simultáneo. Además es habitual que éstos estén controlados por computadora, de modo que se pueden ubicar los máximos para los picos y registrar sus intensidades y la de los fondos correspondientes con una rapidez similar a la que se consigue con espectrómetros dispersivos en energías.