Ecuaciones de estado

Como hemos visto, $T$, $Y$ y $\{µ_j\}$ pueden escribirse en términos de $S,X$ y $\{n_k\}$ (derivando la ecuación fundamental para $U$). Las relaciones que se obtienen se denominan ecuaciones de estado.

Debe tenerse cuidado con el hecho de que una ecuación de estado no contiene toda la información termodinámica posible; sin embargo, el conjunto de todas las ecuaciones de estado equivale a la ecuación fundamental.

El hecho de que la ecuación fundamental sea homogénea de primer orden implica que las ecuaciones de estado son homogéneas de orden cero. Por ejemplo,

$$T(\lambda S,\lambda X,\lambda n_1,\cdots,\lambda n_r) = T(S,X,n_1,\cdots,n_r)\;.$$

Éste es el verdadero concepto de intensivo: en una porción de sistema las variables intensivas valen lo mismo que en todo el sistema (por supuesto, cuando éste es homogéneo). Afortunadamente, esta propiedad concuerda con las ideas previas que teníamos para $Y$ (en particular $P$), $T$ e incluso $µ_j$.

Ya hemos dicho que cuando se trabaja con un sistema simple monocomponente, suelen escribirse las ecuaciones fundamentales por mol ($n=1$), es decir $u=u(s,x)$, con $u=U/n$, $s=S/n$ y $x=X/n \; (v=V/n)$; de este modo, la forma diferencial será

$${\rm d}u = T {\rm d}s + Y {\rm d}x \;.$$

Las variables molares $u,s,x$ suelen referirse como intensivas, aunque debe tenerse presente que la extensividad de las variables originales es el único medio de que se dispone para dar una idea ``cuantitativa'' acerca de un sistema.

Las ecuaciones de estado pueden obtenerse también a partir de la ecuación fundamental para la entropía. En ese caso, los parámetros intensivos resultan definidos de la forma diferencial

$${\rm d}S = \left(\frac{\partial S}{\partial U}\right)_{X,... ...S}{\partial n_j}\right)_{U,X,\{n_{k\neq j}\}} {\rm d}n_j \;,$$

de manera que

$$\left(\frac{\partial S}{\partial U}\right)_{X,\{n_j\}} = \f... ...artial n_j}\right)_{U,X,\{n_{k\neq j}\}} = -\frac{\mu_j}T \;.$$

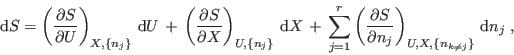
Esta formulación es equivalente a la anterior, y es muy común alternar entre ambas. Cuando es necesario aclarar cuál utilizamos, a esta última la llamamos representación entropía, mientras que a la anterior la denominamos representación energía.