Siguiente: Equilibrio mecánico Subir: Condiciones para el equilibrio Anterior: Ecuaciones de estado
Consideremos nuevamente el cilindro cerrado con un pistón rígido e impermeable a la materia y diatérmico (permite flujo de calor). ![]() y
y ![]() pueden cambiar cumpliendo la condición
pueden cambiar cumpliendo la condición
![]() cte y tomarán los valores que maximicen
cte y tomarán los valores que maximicen
![]() . O sea, alrededor del estado final de equilibrio,
. O sea, alrededor del estado final de equilibrio,
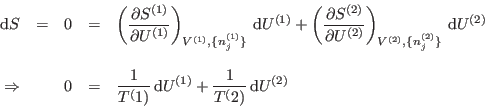
para
![]() arbitrario.
arbitrario.
La condición de equilibrio es, entonces:
![\begin{displaymath}
\fbox{ $\displaystyle \frac{1}{T^{(1)}}=\frac{1}{T^{(2)}}
\rule[-1.75em]{0em}{4em} $ }
\end{displaymath}](img111.png)
Si conocemos las relaciones fundamentales, para cada subsistema ![]() es función de
es función de ![]() , de manera que la ecuación para el equilibrio relaciona
, de manera que la ecuación para el equilibrio relaciona ![]() con
con ![]() , y usando que
, y usando que
![]() cte obtenemos los valores para
cte obtenemos los valores para ![]() y
y ![]() en el estado final. La condición de máximo exige además que se cumpla
en el estado final. La condición de máximo exige además que se cumpla
![]() ; por ahora no examinaremos ese requisito, aunque lo explotaremos más adelante al estudiar las condiciones de estabilidad termodinámica.
; por ahora no examinaremos ese requisito, aunque lo explotaremos más adelante al estudiar las condiciones de estabilidad termodinámica.
Vale la pena destacar que obtuvimos este resultado sin haber utilizado las relaciones fundamentales específicas para el sistema.
Viendo nuestro ejemplo un poco más en detalle, consideremos el caso en que
las temperaturas son casi iguales antes de permitir que fluya el calor, con
![]() . Una vez liberada la restricción la entropía busca
aumentar:
. Una vez liberada la restricción la entropía busca
aumentar:
Notemos que este resultado no depende de que ![]() y
y ![]() hayan
sido parecidas. Si son muy diferentes, puede pensarse en sucesivos procesos
infinitesimales en los que los cambios diferenciales de
hayan
sido parecidas. Si son muy diferentes, puede pensarse en sucesivos procesos
infinitesimales en los que los cambios diferenciales de ![]() y
y
![]() se van acomodando para maximizar continuamente la entropía; el
proceso completo incluiría integrales, pero cada contribución infinitesimal
sería positiva.
se van acomodando para maximizar continuamente la entropía; el
proceso completo incluiría integrales, pero cada contribución infinitesimal
sería positiva.
Otro aspecto interesante de este resultado es que nuestro concepto intuitivo
de temperatura concuerda con la intensividad de nuestra ![]() , como también
ocurre con las nociones de frío y caliente, ya que el calor fluye en la
dirección ``correcta''. Esto nos permite adoptar como temperatura
termodinámica la que hemos introducido a través de las correspondientes
ecuaciones de estado.
, como también
ocurre con las nociones de frío y caliente, ya que el calor fluye en la
dirección ``correcta''. Esto nos permite adoptar como temperatura
termodinámica la que hemos introducido a través de las correspondientes
ecuaciones de estado.
Las posibles escalas de temperatura `absoluta' coinciden en el valor para
![]() y sólo difieren en un factor de conversión; en nuestro caso adoptamos
la escala Kelvin: para el punto triple del agua la temperatura vale
273,16 K.
y sólo difieren en un factor de conversión; en nuestro caso adoptamos
la escala Kelvin: para el punto triple del agua la temperatura vale
273,16 K.
Gustavo Castellano 12/06/2018