Máquina de Carnot

Las máquinas de Carnot son máquinas cíclicas ideales que se han estudiado siempre con asiduidad debido a su relevancia histórica, pero sobre todo porque ayudan a comprender mejor ciertos aspectos importantes de la termodinámica. Estas máquinas constan de dos reservorios de calor a temperaturas $T_1$ y $T_2(>T_1)$, y un sistema auxiliar que se utiliza para extraer calor del reservorio ``caliente'' a $T_2$, transformándolo en trabajo mecánico $W'$ y entregando calor sobrante a $T_1$. El gráfico contiguo corresponde a un ciclo completo de una máquina cuyo sistema auxiliar es un gas.

 

El primer proceso se inicia en el estado $A$ y consiste de una expansión isotérmica en contacto con el reservorio a $T_2$ hasta llegar al estado $B$; durante esta expansión se absorbe una cantidad de calor $Q_2$. A continuación se aisla térmicamente el sistema para realizar una expansión adiabática hasta el estado $C$. Luego se comprime el sistema hasta el estado $D$, manteniéndolo en contacto con el reservorio a $T_1$, de manera que se entrega al mismo una cantidad de calor $Q_1'$. El último proceso de cada ciclo se realiza aislando nuevamente el sistema, compriméndolo hasta retornar al estado inicial $A$.

Las máquinas de Carnot no necesariamente utilizan un gas como sistema auxiliar. En el caso general se tiene una variable intensiva $Y$ asociada con una variable extensiva $X$ característica del sistema, de manera que el diagrama correspondiente al ciclo de Carnot en esta representación tendrá el aspecto cualitativo que se muestra en la figura. Tanto en el diagrama anterior como en este último, el área encerrada por la curva debe representar el trabajo $W'$ realizado por el sistema auxiliar. En el caso general esa área ilustra el valor de la integral $-\oint Y {\rm d}X$, mientras que para el caso de un gas debe representar la integral $+\oint P {\rm d} V$. Es evidente

 

entonces que el sentido de los ciclos en los diagramas debe ser opuesto, ya que el trabajo realizado por el sistema en ambos casos debe ser positivo.

 

Es frecuente también representar el ciclo de Carnot en el plano $T$-$S$. En este caso el diagrama resulta especialmente simple, ya que --como hemos dicho-- los procesos se realizan a $T$ constante o $S$ constante. El área que encierra el ciclo en este diagrama representa la cantidad neta de calor absorbida por el sistema auxiliar. De todos modos, debido a que el sistema realiza un ciclo regresando al estado inicial, $\Delta U=0$ lo que implica que el área mencionada debe coincidir con la correspondiente a la representación anterior, ya que debe cumplirse $\Delta Q=W'$.

 

En cualquiera de estas representaciones puede verse que

$$\begin{eqnarray*} Q_2 &=& T_2 (S_B - S_A) \; \equiv \; T_2 \Delta S \\ Q_1 &=& T_1 (S_D - S_C) \; = \; -T_1 \Delta S \end{eqnarray*}$$

de manera que

$$W' = Q_1 + Q_2 = (T_2-T_1) \Delta S \;.$$

El rendimiento de la máquina de Carnot es entonces

$$\varepsilon = \frac{W'}{Q_2} = 1-\frac{T_1}{T_2} \;,$$

es decir, el mismo rendimiento que el de las máquinas infinitesimales que vimos en la sección anterior.

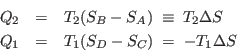
Las máquinas de Carnot son las máquinas térmicas más eficientes que pueden operar entre dos temperaturas determinadas (¡en particular porque son reversibles!). Este resultado se había analizado en cursos anteriores: si existiera una máquina térmica más eficiente que la de Carnot podría utilizársela en conjunción con esta última operada en sentido inverso; el trabajo producido por la máquina super-eficiente puede emplearse para operar la de Carnot, haciendo fluir calor de una fuente fría a una fuente caliente como único resultado de nuestro proceso, violando así uno de los enunciados de la segunda ley de la termodinámica.

Vale la pena notar que las máquinas reales nunca alcanzan la eficiencia termodinámica ideal, valiendo en los casos más favorables un 40% de ésta. Sin embargo, el valor de la eficiencia ideal se utiliza habitualmente como referencia en el diseño de motores.

Vemos que las máquinas de Carnot proveen un medio para medir la temperatura. Hasta el momento sólo la habíamos definido como la derivada de una función abstracta, la entropía. Ahora podemos utilizar el hecho de que

$$\varepsilon = \frac{W'}{Q_2} = 1-\frac{T_1}{T_2}$$

para determinar cocientes de temperaturas a través de la medición de $W'$ y $Q_2$. El hecho de que sólo se midan cocientes de temperaturas significa que las escalas termodinámicas sólo pueden diferir en una constante multiplicativa. Como habíamos dicho antes, lo usual es adoptar la escala Kelvin, que toma como punto de referencia 273,16 K para el punto triple del agua (coexistencia de fase gaseosa, líquida y sólida).

De la misma manera pueden medirse diferencias de entropía, lo cual dejaría indeterminada una constante aditiva para $S$; no obstante, teniendo en cuenta el postulado de Nernst, los respectivos valores quedan completamente determinados, ya que para $T=0$ debe valer $S=0$.