Si tenemos una variable aleatoria 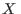 regida por
regida por 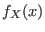 , puede definirse
una nueva variable como el promedio de
, puede definirse
una nueva variable como el promedio de 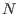 mediciones independientes de
dicha magnitud, es decir,
mediciones independientes de
dicha magnitud, es decir,
La pregunta que nos planteamos es ¿cómo será la distribución de
probabilidades
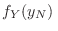 de esta nueva variable estocástica?
de esta nueva variable estocástica?
Para responder este ácido interrogante, estudiemos primero la variable
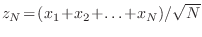 , que es proporcional a
, que es proporcional a 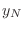 ; analicemos la función característica correspondiente a
; analicemos la función característica correspondiente a 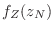
Tomando
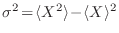 , puede
desarrollarse
, puede
desarrollarse
La exponencial oscilatoria en la integral nos permite ver que
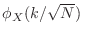 decrece con
decrece con 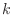 , de manera que
, de manera que
![$\big[\phi_X\big(k/\sqrt{N}\big)\big]^N $](img193.png) decrecerá aún más rápidamente. Si cuando
decrecerá aún más rápidamente. Si cuando
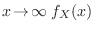 decae de tal forma que todos los
decae de tal forma que todos los
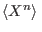 son finitos,
son finitos,
De este modo, podemos reconstruir
Completando cuadrados puede resolverse la integral para obtener
de manera que la densidad de probabilidad para la variable 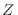 es una gaussiana centrada en
es una gaussiana centrada en
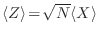 , con una desviación estándar
, con una desviación estándar 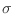 , idéntica a la que tiene la variable
, idéntica a la que tiene la variable 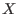 . Para la variable
. Para la variable
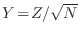 es directo mostrar que
es directo mostrar que
Estos resultados se conocen como teorema del límite central, y nos dicen que, sin importar cuál es la forma de 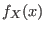 , el valor medio de la variable estocástica
, el valor medio de la variable estocástica 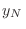 coincide con
coincide con
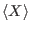 y la distribución
y la distribución
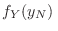 es gaussiana, con
es gaussiana, con
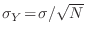 . Vale la pena resaltar que los requisitos que hemos pedido para nuestros
. Vale la pena resaltar que los requisitos que hemos pedido para nuestros 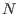 experimentos son: que sean independientes, que los momentos
experimentos son: que sean independientes, que los momentos
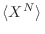 sean finitos y que
sean finitos y que 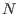 sea grande.
sea grande.
Gustavo Castellano 19/11/2021
![]() regida por
regida por ![]() , puede definirse
una nueva variable como el promedio de
, puede definirse
una nueva variable como el promedio de ![]() mediciones independientes de
dicha magnitud, es decir,
mediciones independientes de
dicha magnitud, es decir,
![]() , que es proporcional a
, que es proporcional a ![]() ; analicemos la función característica correspondiente a
; analicemos la función característica correspondiente a ![]()
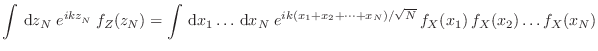
![$\displaystyle \left[\phi_X\left(\frac{k}{\sqrt{N}}\right)\right]^N \;.$](img188.png)
![$\displaystyle \phi_X\left(\frac{k}{\sqrt{N}}\right) =
e^{ik\langle X\rangle/\s...
...e X\rangle/\sqrt{N}}
\left[ 1 - \frac{k^2}{2 N} \sigma^2 + \cdots \right]
$](img190.png)
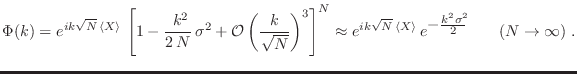
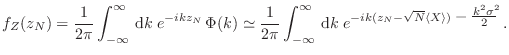
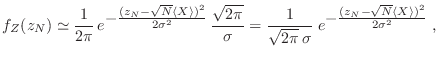
![$\displaystyle \fbox{ $\displaystyle f_Y(y_N) \simeq \frac 1{\sqrt{2\pi}} ...
...frac{N(y_N-\langle X\rangle)^2}{2\sigma^2}}
\rule[-1.75em]{0em}{4em} $ }
$](img201.png)