Siguiente: Teorema del límite central Subir: Distribución binomial Anterior: Distribución de Poisson
Veamos ahora una aplicación típica de la distribución binomial, consistente en un movimiento unidimensional con pasos de longitud fija, hacia adelante (con probabilidad ![]() ) o hacia atrás (con probabilidad
) o hacia atrás (con probabilidad ![]() ). Analicemos el caso particular en que ambos eventos son igualmente probables, es decir,
). Analicemos el caso particular en que ambos eventos son igualmente probables, es decir,
![]() .
.
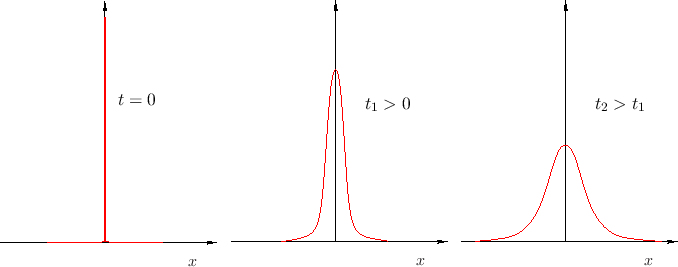
Al cabo de un número grande ![]() de pasos, la distribución de
probabilidades para
de pasos, la distribución de
probabilidades para ![]() pasos hacia adelante será gaussiana, ya que
pasos hacia adelante será gaussiana, ya que
![]() también es grande. El desplazamiento neto será
también es grande. El desplazamiento neto será
![]() , y
como
, y
como
![]() , podemos reescribir
, podemos reescribir
![]() . La distribución de
probabilidades para
. La distribución de
probabilidades para ![]() se obtiene de (3), aunque con esta
notación,
se obtiene de (3), aunque con esta
notación, ![]() sólo puede tomar los valores
sólo puede tomar los valores
![]() . Si
deseamos incluir valores intermedios de
. Si
deseamos incluir valores intermedios de ![]() (pues también son posibles),
es necesario agregar un factor 1/2 “repartiendo” la probabilidad, y evitando
que se pierda la condición de normalización. De este modo obtenemos
(pues también son posibles),
es necesario agregar un factor 1/2 “repartiendo” la probabilidad, y evitando
que se pierda la condición de normalización. De este modo obtenemos
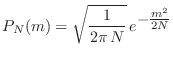
Si la longitud de cada paso es ![]() , el desplazamiento neto real será
, el desplazamiento neto real será
![]() . Al cabo de
. Al cabo de ![]() pasos,
pasos,
![]() , de manera que, como
, de manera que, como
![]() ,
,
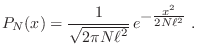
![$\displaystyle \fbox{ $\displaystyle P(x,t) = \frac{1}{2\sqrt{\pi D t}}
e^{\textstyle -\frac{x^2}{4 D t}}
\rule[-1.75em]{0em}{4em} $ }
$](img175.png)
Gustavo Castellano 19/11/2021