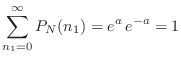Siguiente: Caminata al azar Subir: Distribución binomial Anterior: Distribución gaussiana
En algunos casos, al crecer
![]() , de modo que
, de modo que
![]() . Entonces no es válido tomar
. Entonces no es válido tomar ![]() grande, ya que sus valores serán
próximos a
grande, ya que sus valores serán
próximos a
![]() . De todos modos, puede usarse
la aproximación de Stirling en
. De todos modos, puede usarse
la aproximación de Stirling en
![$\displaystyle \frac{N!}{(N-n_1)!} \approx \frac{\sqrt{N}}{\sqrt{N-n_1}}
\fra...
...\rule[0em]{0em}{1.45em}}
\approx \frac{N^{n_1} e^{-n_1}}{e^{-n_1}} = N^{n_1}
$](img155.png)
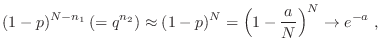
![$\displaystyle \fbox{ $\displaystyle P_N(n_1) = \frac{a^{n_1} e^{-a}}{n_1!}
\rule[-1.75em]{0em}{4em} $ }
$](img157.png)