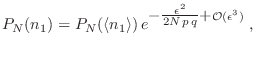Cuando 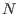 es suficientemente grande y
es suficientemente grande y 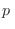 no es demasiado pequeña, de
manera que
no es demasiado pequeña, de
manera que 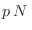 también sea grande, podemos utilizar la fórmula de
Stirling para aproximar
también sea grande, podemos utilizar la fórmula de
Stirling para aproximar
que es válida para 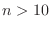 . Si tenemos en cuenta que
. Si tenemos en cuenta que 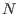 y
y 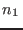 son muy
grandes, reemplazando en la distribución binomial, podemos escribir
son muy
grandes, reemplazando en la distribución binomial, podemos escribir
![$\displaystyle P_N(n_1) = \frac 1{\sqrt{2\pi N}} \exp{ \left[ - n_1\ln\frac{n_1}N -
(N-n_1)\ln\frac{N-n_1}N + n_1\ln p + (N-n_1)\ln(1-p) \right] } \;.$](img140.png) |
(2) |
Es sencillo demostrar que 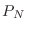 es máximo cuando
es máximo cuando 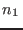 vale
vale
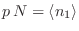 . Podemos desarrollar el exponente de
. Podemos desarrollar el exponente de 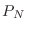 alrededor de
alrededor de
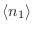 , obteniendo
, obteniendo
donde
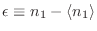 . Como para
. Como para 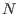 grande
grande
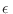 es chico, puede mostrarse que es una buena aproximación
descartar los términos de orden superior al segundo. Recordando que
es chico, puede mostrarse que es una buena aproximación
descartar los términos de orden superior al segundo. Recordando que
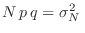 y evaluando correctamente
y evaluando correctamente
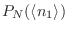 en la expresión (2), se obtiene
en la expresión (2), se obtiene
![$\displaystyle \fbox{ $\displaystyle P_N(n_1) = \frac1{\sqrt{2\pi} \sigma_...
...n_1-\langle n_1 \rangle)^2}{2 \sigma_N^2}}
\rule[-1.75em]{0em}{4.5em} $ }$](img149.png) |
(3) |
Esta es la conocida distribución gaussiana, y tiene la particularidad
de que queda absolutamente determinada mediante
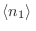 y
y
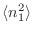 .
.
Gustavo Castellano 19/11/2021
![]() es suficientemente grande y
es suficientemente grande y ![]() no es demasiado pequeña, de
manera que
no es demasiado pequeña, de
manera que ![]() también sea grande, podemos utilizar la fórmula de
Stirling para aproximar
también sea grande, podemos utilizar la fórmula de
Stirling para aproximar