Distribución binomial

Frecuentemente nos enfrentamos con el caso de muchos experimentos que dan como resultado sólo dos valores posibles. Denotamos entonces $p$ y $q$ a las probabilidades para cada resultado, que satisfacen la condición de normalización $p+q=1$.

Al cabo de un número $N$ de experimentos, tendremos respectivamente $n_1$ y $n_2$ resultados, que cumplen con la relación $n_1+n_2=N$. Si estamos interesados en tener $n_1$ experimentos con el primer resultado en un orden determinado, la correspondiente probabilidad será $p^{n_1}q^{n_2}$. Si en cambio no nos interesa el orden, la probabilidad de tener cualquier combinación $n_1,n_2$ está dada por la llamada distribución binomial

$$P_N(n_1)= \left(\!\begin{array}{l}N n_1\end{array}\!\right) p^{n_1} q^{n_2}\;.$$

Es fácil verificar que esta distribución está normalizada, pues

$$\sum_{n_1=0}^N P_N(n_1) = \sum_{n_1=0}^N \left(\! \begin{array}{l}N n_1\end{array}\!\right) p^{n_1} q^{N-n_1} = (p+q)^N = 1 \;.$$

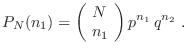
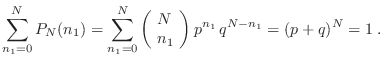
Podemos evaluar el primer momento, teniendo en cuenta que

$$\langle n_1 \rangle = \sum_{n_1=0}^N n_1 \! \left(\!\begin{array... ...= p \frac{\partial }{\partial p} \left[ \sum_{n_1=0}^N P_N(n_1) \right] \;;$$

como el término entre corchetes es $(p+q)^N$, resulta

$$\langle n_1 \rangle = p N \;.$$

Se deja como divertido ejercicio para el lector mostrar que, análogamente, el segundo momento resulta

$$\langle n_1^2 \rangle = (N p)^2 + N p q \;.$$

Con estos dos momentos evaluamos la varianza o la desviación estándar

$$\sigma_N=\sqrt{N p q} \;.$$

Mucho más interesante resulta analizar la desviación estándar relativa

$$\frac{\sigma_N}{\langle n_1 \rangle}=\sqrt{\frac qp}\; \sqrt{\frac 1N} \;.$$

Aquí vemos que este valor se reduce a medida que crece $N$; un valor pequeño de $\sigma_N/\langle n_1 \rangle$ indica que cualquier resultado $n_1$ tomará valores muy próximos al valor medio $p N$. Dicho en otras palabras, a medida que $N$ crece, $n_1/N \simeq \langle n_1 \rangle/N = p$.