Siguiente: Distribución binomial Subir: Variables aleatorias o estocásticas Anterior: Variables estocásticas continuas
Si ![]() e
e ![]() son variables estocásticas sobre un espacio muestral
son variables estocásticas sobre un espacio muestral ![]() , con
, con
![]() e
e
![]() , el conjunto
, el conjunto
![]() estará conformado por los pares ordenados
estará conformado por los pares ordenados
![]()
![]()
![]()
![]() y será un “espacio de probabilidades”, de modo que a cada par ordenado
y será un “espacio de probabilidades”, de modo que a cada par ordenado
![]() asignamos una probabilidad conjunta
asignamos una probabilidad conjunta
![]() .
.
Por supuesto, esa definición vale también para variables continuas. Teniendo
la precaución de sustituir integrales por sumatorias cuando corresponda,
escribiremos el desarrollo que sigue para el caso de variables continuas.
Cuando tenemos la probabilidad conjunta ![]() , podemos obtener la
distribución para una de las variables integrando todos los valores posibles
para la otra:
, podemos obtener la
distribución para una de las variables integrando todos los valores posibles
para la otra:
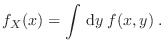
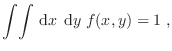
La interdependencia entre estas dos variables estocásticas se evalúa
mediante la covarianza de ![]() e
e ![]() :
:
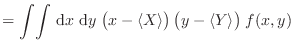 |
||
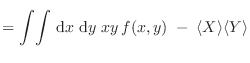 |
||
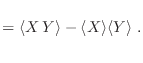 |
También suele usarse la correlación de ![]() e
e ![]() , definida como
, definida como
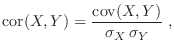
En el caso en que ![]() e
e ![]() son independientes, se satisface que
son independientes, se satisface que
A veces partimos de varias variables estocásticas y necesitamos información
sobre una nueva variable estocástica ![]() , función de aquéllas. Por ejemplo,
supongamos que contamos con la densidad de probabilidad conjunta
, función de aquéllas. Por ejemplo,
supongamos que contamos con la densidad de probabilidad conjunta ![]() para las variables
para las variables ![]() e
e ![]() , que están conectadas con
, que están conectadas con ![]() mediante la
relación
mediante la
relación ![]() . Como señalamos para el caso de una variable, puede
mostrarse que
. Como señalamos para el caso de una variable, puede
mostrarse que
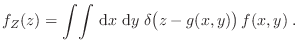
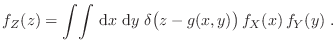
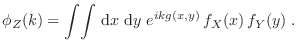
Gustavo Castellano 19/11/2021