Siguiente: Probabilidades conjuntas Subir: Variables aleatorias o estocásticas Anterior: Variables estocásticas discretas
Cuando la variable ![]() puede tomar valores continuos, la distribución debe
ser una función continua a trozos, de modo que la probabilidad de tener un
valor
puede tomar valores continuos, la distribución debe
ser una función continua a trozos, de modo que la probabilidad de tener un
valor
![]() sea el área bajo la curva
sea el área bajo la curva ![]() en ese intervalo:
en ese intervalo:
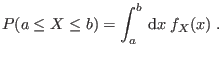
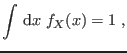
Análogamente al caso de variables discretas, la definición del
![]() -ésimo momento en este caso es
-ésimo momento en este caso es
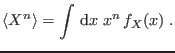
El conocimiento de todos los momentos
![]() implica el
conocimiento completo de
implica el
conocimiento completo de ![]() . Esto se ve fácilmente
introduciendo la función característica
. Esto se ve fácilmente
introduciendo la función característica
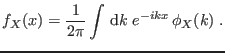
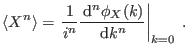
Otra alternativa que puede ser interesante, dependiendo del problema encarado,
involucra una expansión de la función característica
![]() en
término de los cumulantes de orden
en
término de los cumulantes de orden ![]()
![]() , definidos mediante la
relación
, definidos mediante la
relación
![$\displaystyle \phi_X(k) = \exp \left[\sum_{n=1}^\infty\frac{(ik)^n}{n!} C_n(X)\right] \;.
$](img78.png)
A menudo necesitamos conocer la densidad de probabilidad en términos de la
variable estocástica ![]() . Como los valores medios de cualquier función
deben coincidir al calcularlos en términos de
. Como los valores medios de cualquier función
deben coincidir al calcularlos en términos de ![]() o
o ![]() , el entrenado
lector puede mostrar que debe satisfacerse la relación
, el entrenado
lector puede mostrar que debe satisfacerse la relación
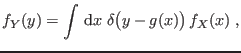
Gustavo Castellano 19/11/2021