La evolución de sistemas clásicos (basado en el texto de Reichl)

Hemos dicho que la Mecánica Estadística estudia sistemas con muchos grados de libertad, como es el caso de $N$ partículas en un recipiente, o $N$ sitios de red interactuando entre sí. En un enfoque clásico, las ecuaciones de Hamilton pueden utilizarse para predecir la evolución del sistema, que estará caracterizado por $3N$ coordenadas y $3N$ impulsos generalizados (ignoramos grados de libertad internos).

Para realizar este análisis es útil introducir el concepto de espacio de las fases $\Gamma$, en este caso de $6N$ dimensiones, en el que cada punto ${X}$$^N$ contiene las $3N$ coordenadas y los $3N$ momentos $($${q}$$^N$${p}$$^N)$. Suele llamarse a cada uno de estos posibles estados “microestados”, para hacer hincapié en el hecho de que dan información microscópica del sistema, a diferencia de los “macroestados” que estudia la termodinámica en general.

Si el valor de ${X}$$^N$ es conocido en algún instante, las ecuaciones de Hamilton nos proveen ${X}$$^N$ para cualquier instante posterior:

   $$\mbox{\boldmath${\dot{p}}$}$$$$_j = - \frac{\partial H^N}{\partial\mbox{\boldmath${q}$}_j} \;; ... ...ldmath${\dot{q}}$}_j = \frac{\partial H^N}{\partial\mbox{\boldmath${p}$}_j}\;,$$

donde $H^N$ es el hamiltoniano del sistema y el subíndice señala a la $j$-ésima partícula. Sabemos además que cuando este no depende explícitamente del tiempo, $H^N($${X}$$^N)\!=\!E$ es una constante de movimiento, la energía, y se dice que el sistema es conservativo.

El microestado del sistema está representado entonces por un punto en el espacio de las fases que se mueve según las ecuaciones anteriores. Como el estado ${X}$$^N$ está perfectamente determinado por las condiciones iniciales para el sistema, sabemos que las trayectorias que describe nunca se cruzan en el espacio de las fases.

Cuando trabajamos con sistemas “termodinámicos” no se pueden especificar completamente sus microestados, de manera que siempre existe cierto grado de incertidumbre respecto de las condiciones iniciales. Por este motivo es razonable considerar que ${X}$$^N$ es una variable estocástica $6N$-dimensional. Puede conocerse algo acerca de su valor medio, e incluso sobre su dispersión, pero hasta que no se realizara una “medición” (ideal) no se podría determinar el valor concreto que toma esta variable. Como toda variable estocástica, ${X}$$^N$ estará regida por una densidad de probabilidad $\rho($${X}$$^N,t)$, de manera que $\rho($${X}$$^N,t) {\rm d}$${X}$$^N$ es la probabilidad de que el microestado del sistema esté en un entorno ${\rm d}$${X}$$^N$ de ${X}$$^N$ en el instante $t$.

La condición de normalización

$$\int_{\Gamma} {\rm d}$$$$\mbox{\boldmath${X}$}$$$$^N\; \rho($$$$\mbox{\boldmath${X}$}$$$$^N,t) = 1$$

debe cumplirse para cualquier instante $t$, ya que el estado del sistema debe estar en alguna región de $\Gamma$. La probabilidad de tener en el instante $t$ un estado en la región $R\subset\Gamma$ es

$$P(R) = \int_R {\rm d}$$$$\mbox{\boldmath${X}$}$$$$^N\; \rho($$$$\mbox{\boldmath${X}$}$$$$^N,t) \;.$$

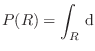
Si en algún momento la incertidumbre sobre ${X}$$^N$ es pequeña, $\rho$ estará muy localizada alrededor del estado más probable, anulándose rápidamente al abandonar un entorno pequeño del mismo. A medida que transcurre el tiempo, es posible que la distribución permanezca muy ajustada, aunque el máximo quizás se desplace en el espacio de las fases, de manera que no se pierda información sobre el sistema; por el contrario, puede ocurrir que se esparza gradualmente, transformándose incluso en una distribución bastante uniforme, con lo cual se perdería la información por completo.

Aunque no es demasiado lo que conocemos sobre dinámica de sistemas continuos, veremos cómo puede establecerse una analogía entre la densidad de probabilidad en $\Gamma$ y la masa en el caso de un fluido incompresible. Para comenzar, notemos que la condición de normalización equivale a la conservación de la materia. De la expresión anterior podemos analizar cómo cambia $P(R)$ con el tiempo, teniendo en cuenta que como un todo debe conservarse la probabilidad. Cualquier aumento en la probabilidad contenida en la región $R$ debe igualarse a la cantidad de probabilidad que fluye hacia dentro de ese volumen en $\Gamma$:

$$\frac{ {\rm d} P(R)}{ {\rm d} t     } = - \oint_S \rho($$$$\mbox{\boldmath${X}$}$$$$^N,t)\;$$   $$\mbox{\boldmath${\dot{X}}$}$$$$^N$$   $$\mbox{\boldmath${\cdot}$}$$$${\rm d}$$$$\mbox{\boldmath${S}$}$$$$^N \;,$$

donde ${\dot{X}}$$^N\equiv($${\dot{q}}$$^N$${\dot{p}}$$^N)$, de manera que el último miembro representa el flujo saliente a través de la superficie $S$ que encierra a $R$. Para evaluar este flujo, podemos recurrir al teorema de Gauss, reescribiendo la expresión anterior como

$$\int_R \frac{\partial \rho(\mbox{\boldmath${X}$}^N,t)}{\partia... ...t) \mbox{\boldmath${\dot{X}}$}^N\right) {\rm d}\mbox{\boldmath${X}$}^N \;,$$

donde

$$\nabla_{\!\mbox{\footnotesize\boldmath$X$}^N}\equiv \left(\frac{\... ...p}$}_1},\cdots, \frac{\partial }{\partial\mbox{\boldmath${p}$}_N}\right) \;,$$

y $\nabla_{\!\mbox{\footnotesize\boldmath $X$}^N}\mbox{\boldmath ${\cdot}$}\left( \right)$ es la divergencia en $\Gamma$. Como la igualdad anterior debe cumplirse para cualquier $R\subset\Gamma$, entonces deben igualarse los integrandos, obteniéndose la celebérrima ecuación de continuidad

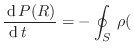
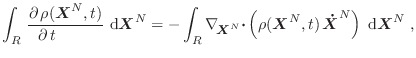
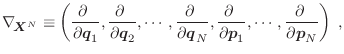
$${\fbox{ $\displaystyle \frac{\partial }{\partial t}\rho(\mb... ...mbox{\boldmath ${\dot{X}}$}^N\right) = 0 \rule[-1.8em]{0em}{4em}$ } }$$

El significado de esta ecuación es similar al que deducíamos en Electromagnetismo, donde habíamos partido considerando la conservación de la carga.

Para nuestro caso, en que $\rho$ es la densidad de probabilidad en el espacio de las fases, $\nabla_{\!\mbox{\footnotesize\boldmath $X$}^N}\mbox{\boldmath ${\cdot}$}\mbox{\boldmath ${\dot{X}}$}^N\!=\!0$; es directo inferir este resultado explicitando

$$\nabla_{\!\mbox{\footnotesize\boldmath $X$}^N}\mbox{\boldmath ${\... ...l\mbox{\boldmath ${\dot{p}}$}_j}{\partial\mbox{\boldmath ${p}$}_j} \right) \;,$$

que se anula en virtud de las ecuaciones de Hamilton que recordamos más arriba. Por lo tanto la ecuación de continuidad puede escribirse como

$$\frac{\partial\rho}{\partial t} = - \mbox{\boldmath${\dot{X}}$} ^N \mbox{\boldmath${\cdot}$} \nabla_{\!\mbox{\footnotesize\boldmath$X$}^N}\rho \;.$$ (4)

Esta derivada expresa los cambios temporales de $\rho$ en un entorno fijo de $\Gamma$. Si deseamos analizar la evolución de $\rho$ a medida que se desplaza el fluido, debemos recurrir a la derivada total o convectiva

$$\frac{ {\rm d} }{ {\rm d} t} = \frac{\partial }{\partial t} +$$   $$\mbox{\boldmath${\dot{X}}$}$$$$^N$$   $$\mbox{\boldmath${\cdot}$}$$$$\nabla_{\!\mbox{\footnotesize\boldmath$X$}^N}$$

En nuestro caso, esto se traduce como

$$\frac{ {\rm d} \rho}{ {\rm d} t} = 0\;.$$

Lo que significa esta identidad es que $\rho$ se mantiene constante alrededor de un punto del “fluido” en movimiento. Es otra manera de identificar la densidad de probabilidad como fluido incompresible.

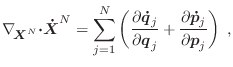
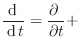
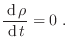
Utilizando las ecuaciones de Hamilton y definiendo

$$\hat{\cal H} \equiv \sum_{j=1}^N \left(\frac{\partial H^N}{\part... ...boldmath${\cdot}$}\frac{\partial }{\partial\mbox{\boldmath${p}$}_j}\right) \;,$$

la ecuación de continuidad (4) puede reescribirse como

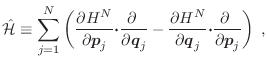
$$\frac{\partial\rho}{\partial t} = - \hat{\cal H}\rho = - \left[H^N,\rho \right]\;,$$

donde $[\cdot ,\cdot]$ representa el corchete de Poisson. La identidad anterior para la evolución temporal de $\rho$ suele escribirse en términos del operador de Liouville $\hat L\equiv-i\hat{\cal H}$:

$${\fbox{ $\displaystyle i \frac{\partial \rho}{\partial t} = \hat L \rho \rule[-1.8em]{0em}{4em}$ } }$$

Esta expresión es conocida como ecuación de Liouville, y la solución formal puede escribirse como

$$\rho( \mbox{\boldmath${X}$} ^N,t) = e^{-it\hat L} \rho( \mbox{\boldmath${X}$} ^N,0) \;,$$ (5)

donde $\rho($${X}$$^N,0)$ es la condición inicial para $\rho$. Puede mostrarse que el operador $\hat L$ es hermitiano, de manera que para la ecuación de autovectores

$$\hat L f_j = \lambda_j f_j \;,$$

sus autovalores $\lambda_j$ son reales, y los autovectores $f_j$ forman una base ortonormal en el espacio de Hilbert donde definimos $\rho$. Podemos expandir en esa base la condición inicial

$$\rho($$$$\mbox{\boldmath${X}$}$$$$^N,0) = \sum_j C_j f_j($$$$\mbox{\boldmath${X}$}$$$$^N) \;,$$

de manera que

$$\hat L \rho($$$$\mbox{\boldmath${X}$}$$$$^N,0) = \sum_j C_j \lambda_j f_j($$$$\mbox{\boldmath${X}$}$$$$^N) \;.$$

Entonces, la ecuación (5) toma la forma

$$\rho($$$$\mbox{\boldmath${X}$}$$$$^N,t) = \sum_j e^{-it\lambda_j} C_j f_j($$$$\mbox{\boldmath${X}$}$$$$^N) \;.$$

Como los autovalores $\lambda_j$ son reales, la densidad de probabilidad tendrá siempre un comportamiento oscilatorio, sin lograrse reproducir el decaimiento al equilibrio que se observa en los sistemas reales. Además, como las ecuaciones de Hamilton son reversibles en el tiempo, si en algún momento el sistema arribara al equilibrio, esta ecuación nos dice que podría recorrer el camino inverso, si se cambian todos los ${p}$ por $-$${p}$ hasta retornar a la condición inicial.

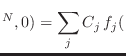
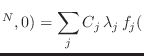
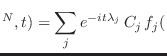
El problema de obtener el equilibrio termodinámico a partir de la dinámica que describen las ecuaciones de la mecánica clásica evidentemente no es posible. La ecuación de Liouville no nos permite conocer el camino mediante el cual se llega al equilibrio, aunque nos proporciona una condición que debe satisfacerse en un sistema que ya alcanzó un estado estacionario, pues en ese caso $\rho$ no depende explícitamente del tiempo y por lo tanto $\hat L\rho\!=\!0$, o lo que es equivalente, $[H_N,\rho]\!=\!0$.