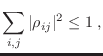El operador densidad (basado en el texto de Nazareno)

Veremos a continuación cuánto se puede avanzar mediante una descripción cuántica, para lo cual introduciremos la idea de ensamble¹, definiéndolo como una colección de $M$ sistemas físicos idénticos macroscópicamente, cada uno ocupando los diferentes microestados accesibles.

La idea es que el valor medio temporal de cualquier variable dinámica del sistema es igual al promedio de esa variable sobre el ensamble. Esta propiedad, denominada ergodicidad puede no ser válida en algunos sistemas, aunque sí lo será en todos los casos que estudiemos a lo largo de este curso. Si bien existen herramientas formales para demostrar cuándo un sistema es ergódico, nosotros descansaremos en el hecho de que en todos los casos que analizaremos, esta propiedad será siempre aceptable para el sentido común.

Cada sistema de nuestro ensamble tendrá un estado cuántico descripto por la función de onda $\vert k,t\rangle$, donde $k$ representa todos los números cuánticos que caracterizan al sistema. El valor de expectación de una variable dinámica $\hat A$ cuando el sistema se halla en ese estado estará dado por

$$A_k(t) = \langle k,t\vert\hat A\vert k,t\rangle \;,$$

siempre que tomemos estados normalizados ( $\langle k,t\vert k,t\rangle\!=\!1$). El promedio de $\hat A$ sobre todo el ensamble será

$$\langle \hat A\rangle_M(t) = \frac 1M \sum_{\rm ens}\langle k,t\vert\hat A\vert k,t\rangle = \sum_k \omega_k A_k(t)\;,$$

donde hemos introducido el peso estadístico $\omega_k\!=\!M_k/M$ (evidentemente, $\sum_k\omega_k\!=\!1$); aquí $M_k$ representa el número de sistemas que en el estado $\vert k,t\rangle$, para los cuales el valor de expectación de $\hat A$ es $A_k$.

Si definimos el operador densidad

$$\hat\rho = \sum_k \omega_k \vert k,t\rangle \langle k,t\vert \;,$$

puede verse que para cualquier variable $\hat A$ se puede escribir

$$\langle \hat A\rangle_M(t) = {\rm Tr}\big(\hat\rho\hat A\big) \;.$$

Es fácil mostrar que $\hat\rho ^\dagger\!=\!\hat\rho$, es decir, es un operador hermitiano. También resulta inmediato verificar que ${\rm Tr} (\hat\rho)\!=\!1$. Otra propiedad de este operador es que, independientemente de la base elegida, son no-negativos sus elementos diagonales $\rho_i\equiv\rho_{ii}$ (la demostración es directa a partir de la definición, y también se deja como ejercicio). De esto resulta que como

$${\rm Tr} (\hat\rho) = 1 = \sum_i \rho_i \;\Rightarrow\; 0 \le \rho_i \le 1 \;.$$

Por último destaquemos la propiedad de que como existe una base en la que $\hat\rho$ es diagonal, esta última desigualdad implica que ${\rm Tr}\left(\hat\rho ^2\right)\le 1$, de manera que en una base arbitraria

$$\sum_{i,j} \vert\rho_{ij}\vert^2 \le 1 \;,$$

es decir, todos los elementos de $\hat\rho$ son acotados.