Ecuación de Liouville
Sabemos que, si 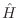 es el hamiltoniano de nuestro sistema y
es el hamiltoniano de nuestro sistema y
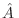 es independiente de
es independiente de 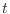 , para cada estado
, para cada estado
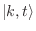 de nuestro ensamble
de nuestro ensamble
donde no debe confundirse el conmutador con el corchete de Poisson. Por otro
lado, como
podemos escribir
de modo que
(para verificar la última identidad sólo es necesario recordar propiedades simples de una traza, como
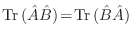 ). Como esta relación es válida para cualquier
). Como esta relación es válida para cualquier 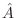 , entonces debe cumplirse la ecuación de Liouville cuántica (o ecuación de Liouville - von Neumann)
, entonces debe cumplirse la ecuación de Liouville cuántica (o ecuación de Liouville - von Neumann)
También en este caso podemos definir el operador de Liouville
En este caso no diremos nada acerca de la hermiticidad de 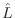 ,
aunque nuevamente es posible escribir la solución formal como
,
aunque nuevamente es posible escribir la solución formal como
El último término puede obtenerse desarrollando
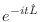 como una serie de potencias y luego explicitando el
binomio de Newton correspondiente a las potencias del conmutador
como una serie de potencias y luego explicitando el
binomio de Newton correspondiente a las potencias del conmutador
![$[\hat
H,\cdot ]$](img335.png) . Si representamos a
. Si representamos a
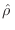 en una base ortonormal de
autofunciones de
en una base ortonormal de
autofunciones de
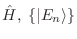 , recordando que
, recordando que
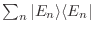 es el operador identidad, resulta
es el operador identidad, resulta
Esta expresión nos permite ver claramente que la descripción cuántica también provee soluciones oscilatorias para la evolución de nuestro sistema, ya que
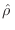 consiste de una suma de términos que oscilan con distinta frecuencia.
consiste de una suma de términos que oscilan con distinta frecuencia.
En cambio podemos observar que cuando se ha alcanzado el estado estacionario debe cumplirse
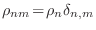 , es decir
, es decir
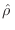 debe ser diagonal en esta representación, para que se anulen los términos oscilatorios. Esto es posible si en el equilibrio
debe ser diagonal en esta representación, para que se anulen los términos oscilatorios. Esto es posible si en el equilibrio
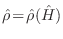 , lo cual era evidente de la ecuación de Liouville independiente de
, lo cual era evidente de la ecuación de Liouville independiente de  , pues entonces
, pues entonces
![$[\hat H,\hat\rho]\!=\!0$](img341.png) .
.
Gustavo Castellano 19/11/2021
![]() es el hamiltoniano de nuestro sistema y
es el hamiltoniano de nuestro sistema y
![]() es independiente de
es independiente de ![]() , para cada estado
, para cada estado
![]() de nuestro ensamble
de nuestro ensamble
![$\displaystyle i\hbar \frac{ {\rm d} }{ {\rm d}t}
\big\langle k,t\big\vert\h...
...\rangle =
\big\langle k,t\big\vert[\hat A,\hat H]\big\vert k,t\big\rangle \;,
$](img325.png)
![$\displaystyle i\hbar \frac{ {\rm d} }{ {\rm d}t}\langle \hat A\rangle_M =
i...
...[\hat A,\hat H]\big\vert k,t\big\rangle
= \langle[\hat A,\hat H]\rangle_M \;,
$](img327.png)
![$\displaystyle i\hbar {\rm Tr}\left(\frac{\partial\hat\rho}{\partial t}
\hat A...
...t\rho
[\hat A,\hat H] \big) =
{\rm Tr}\big([\hat H,\hat\rho] \hat A\big)
$](img328.png)
![$\displaystyle i\hbar \frac{\partial\hat\rho}{\partial t} = [\hat H,\hat\rho]
$](img330.png)
![$\displaystyle \hat L = \frac 1\hbar [\hat H,\cdot ] \qquad \Rightarrow \qquad
i \frac{\partial\hat\rho}{\partial t} = \hat L \hat\rho \;.
$](img331.png)
![]() ,
aunque nuevamente es posible escribir la solución formal como
,
aunque nuevamente es posible escribir la solución formal como
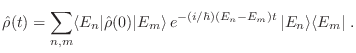
![]() , es decir
, es decir
![]() debe ser diagonal en esta representación, para que se anulen los términos oscilatorios. Esto es posible si en el equilibrio
debe ser diagonal en esta representación, para que se anulen los términos oscilatorios. Esto es posible si en el equilibrio
![]() , lo cual era evidente de la ecuación de Liouville independiente de
, lo cual era evidente de la ecuación de Liouville independiente de ![]() , pues entonces
, pues entonces
![]() .
.