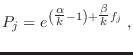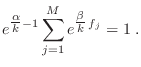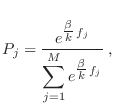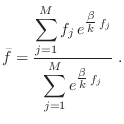Este principio queda prácticamente enunciado con el título que hemos
elegido:
El sentido de este principio ha quedado explicitado en los ejemplos
anteriores: de algún modo señala que no hay razón para privilegiar un estado
particular de antemano.
El procedimiento habitual para maximizar la entropía consiste en recurrir al
método variacional, imponiendo los vínculos mediante multiplicadores de
Lagrange. Veamos primero el ejemplo de hallar la distribución de
probabilidad en nuestro conjunto de 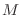 eventos bajo la única imposición
de la normalización,
eventos bajo la única imposición
de la normalización,
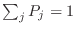 . Debemos exigir que alrededor de la
distribución
. Debemos exigir que alrededor de la
distribución 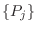 que maximiza (6) las variaciones
virtuales se anulen:
que maximiza (6) las variaciones
virtuales se anulen:
donde 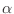 es el multiplicador de Lagrange asociado con la
normalización. Permitimos entonces variaciones infinitesimales
es el multiplicador de Lagrange asociado con la
normalización. Permitimos entonces variaciones infinitesimales
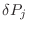 en las probabilidades (como si fueran independientes), obteniendo
en las probabilidades (como si fueran independientes), obteniendo
Como esto debe anularse para cualquier conjunto de variaciones
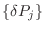 arbitrarias, entonces debe anularse el término entre corchetes para cada
arbitrarias, entonces debe anularse el término entre corchetes para cada 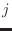 , con lo cual resulta
, con lo cual resulta
es decir, todos los estados tienen la misma probabilidad, que por la
condición de normalización no pueden sino valer 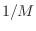 . En efecto,
escribiendo explícitamente
. En efecto,
escribiendo explícitamente
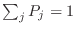 podemos además encontrar el
valor para el multiplicador
podemos además encontrar el
valor para el multiplicador 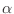 :
:
En el caso de contar con algún vínculo adicional
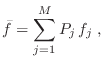 |
(7) |
el proceso de maximización es similar, sólo que debemos acompañar esta nueva
restricción con otro multiplicador de Lagrange 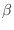 , resultando
, resultando
Obtenemos entonces
y cuando imponemos la condición de normalización vemos que debe cumplirse
Definimos entonces la función partición
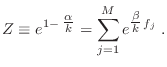 |
(8) |
Sustituyendo en la expresión anterior, obtenemos
donde se evidencia que la distribución 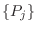 está normalizada. Falta
aún determinar el valor del multiplicador
está normalizada. Falta
aún determinar el valor del multiplicador 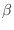 , que puede obtenerse
utilizando el vínculo (7)
, que puede obtenerse
utilizando el vínculo (7)
Despejando de aquí 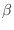 , podemos encontrar también el valor de
, podemos encontrar también el valor de 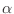 a través de (8). La generalización para el caso de mayor número de
vínculos es inmediata, y sólo debe tenerse la precaución de no
sobredeterminar el sistema.
a través de (8). La generalización para el caso de mayor número de
vínculos es inmediata, y sólo debe tenerse la precaución de no
sobredeterminar el sistema.
Gustavo Castellano 19/11/2021
![\fbox{\rule[-2em]{0em}{4.5em}\rule{1.5em}{0em}
\parbox{14.5cm}{\sl La entropía ...
...ma alcanza el
máximo compatible con los vínculos impuestos. }\rule{1.5em}{0em}}](img364.png)
![]() eventos bajo la única imposición
de la normalización,
eventos bajo la única imposición
de la normalización,
![]() . Debemos exigir que alrededor de la
distribución
. Debemos exigir que alrededor de la
distribución ![]() que maximiza (6) las variaciones
virtuales se anulen:
que maximiza (6) las variaciones
virtuales se anulen:
![$\displaystyle \delta \left[ - k \sum_{j=1}^M P_j \ln P_j +
\alpha \sum_{j=1}^M P_j \right] = 0 \;,
$](img366.png)
![$\displaystyle \sum_{j=1}^M \delta P_j \left[ - k \ln P_j + (\alpha-k) \right] = 0 \;.
$](img369.png)

![$\displaystyle \sum_{j=1}^M \delta P_j \left[ -k\ln P_j+(\alpha-k)+\beta f_j\right ]=0 \;.
$](img376.png)