Entropía de información

Para avanzar con nuestra descripción, introduzcamos el operador $-k \ln\hat\rho$, donde $k$ es una constante. El valor medio de este operador en un ensamble es

$$S \equiv \langle -k \ln\hat\rho \rangle_M = - k \; {\rm Tr} (\hat\rho \ln\hat\rho) = - k \sum_j \rho_j\ln\rho_j \;;$$

el último miembro corresponde a una base que diagonaliza a $\hat\rho$. Vemos que $S\ge0$, ya que los elementos diagonales de $\hat\rho$ cumplen $0\le\rho_j\le1$ (cualquiera sea la base escogida).

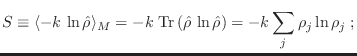
En el caso de tener un ensamble puro, en esta representación todos los elementos de $\hat\rho$ se anulan excepto uno que vale 1, de modo que $S=0$. En otras palabras, cuando poseemos la máxima información sobre el sistema, $S$ alcanza su valor mínimo. Por otro lado, en la próxima sección veremos que $S$ alcanza el valor máximo cuando todas las probabilidades $\rho_j$ son iguales, es decir, cuando poseemos el mínimo de información sobre el estado de un sistema.

El valor de $S$ cuantifica de alguna manera la falta de información o la incertidumbre respecto de un sistema. Esta magnitud se denomina entropía de información o entropía estadística², y en general para un sistema regido por una distribución de probabilidades $\{P_j\}$ se define directamente como

$$S \equiv - k \sum_{j=1}^M P_j \ln P_j \;,$$ (6)

Si los $M$ estados accesibles para el sistema son equiprobables,

$$P_j = \frac 1M \qquad\Rightarrow\qquad S = k \ln M \;,$$

de manera que $S$ es creciente con $M$. Otra propiedad importante es la aditividad, para lo cual imaginamos dos sistemas independientes: el $A$, con $\ell$ resultados posibles cuyas probabilidades son $p_i$ ( $i\!=\!1,\dots,\ell$) y el $B$, con $m$ resultados posibles cuyas probabilidades son $q_j$ ( $j\!=\!1,\dots,m$). Como los sistemas son independientes, la probabilidad de tener simultáneamente el resultado $i$ para el sistema $A$ y $j$ para el $B$ es $\pi_{ij}\!=\!p_i q_j$ ($\{p_i\}$ y $\{q_j\}$ están normalizadas, con lo cual $\{\pi_{ij}\}$ queda automáticamente normalizada). La entropía para el sistema conjunto es

$$S_{A\!+\!B} = - k\! \sum_{i,j=1}^{\ell,m} \pi_{ij} \ln\pi_{ij} = ... ...gris}{\underbrace{\textcolor{black}{\sum_{i=1}^\ell p_i}}_1}} = S_A + S_B \;.$$

Cuando consideremos sistemas termodinámicos, veremos que puede haber cierta interdependencia entre subsistemas, sin que esto afecte la aditividad de la entropía (ni de otras variables extensivas como la energía interna, el momento magnético total, etc.).

En el caso de trabajar con variables continuas el desarrollo anterior se mantiene, excepto por el correspondiente reemplazo de sumatorias por integrales.