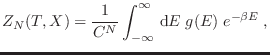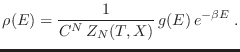Cuando el sistema analizado se describe adecuadamente mediante un enfoque
clásico, debemos maximizar la expresión
agregando a la condición de normalización
la restricción para el valor medio de la energía
Nuevamente utilizamos el método variacional acompañando estos dos vínculos
con multiplicadores de Lagrange
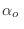 y
y
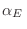 respectivamente.
Exigimos entonces que las variaciones virtuales alrededor del máximo
correspondan a un extremo
respectivamente.
Exigimos entonces que las variaciones virtuales alrededor del máximo
correspondan a un extremo
Como las variaciones
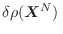 deben ser arbitrarias, esta
condición se traduce como
deben ser arbitrarias, esta
condición se traduce como
![$\displaystyle \alpha_o + \alpha_E H(\bm{X}^N) - k \ln [C^N\rho(\bm{X}^N)] - k = 0 \;,$](img518.png) |
(13) |
de modo que
En esta expresión aún desconocemos cuánto deben valer los multiplicadores
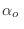 y
y 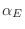 . Para determinarlos es necesario recurrir a las
condiciones de vínculo. En primer lugar, la condición de normalización nos
conduce a definir la función partición
. Para determinarlos es necesario recurrir a las
condiciones de vínculo. En primer lugar, la condición de normalización nos
conduce a definir la función partición
Vemos que esta expresión relaciona los dos multiplicadores desconocidos, y
para determinar el valor de 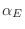 , multiplicamos la expresión
(13) por
, multiplicamos la expresión
(13) por
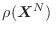 y luego integramos en
y luego integramos en 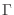 ,
obteniendo
,
obteniendo
Esta relación entre 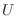 y
y 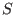 evoca la definición que aceptamos para el
potencial de Helmholtz
evoca la definición que aceptamos para el
potencial de Helmholtz
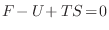 , lo que sugiere identificar
, lo que sugiere identificar
De esta manera, introduciendo el parámetro
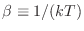 , la función
partición toma la forma
, la función
partición toma la forma
donde hemos reemplazado 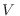 por
por 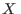 para incluir el caso general de
variable extensiva asociada con el trabajo mecánico. El ensamble canónico
queda completamente determinado por la expresión anterior y la distribución
de probabilidades, que finalmente toma la forma
para incluir el caso general de
variable extensiva asociada con el trabajo mecánico. El ensamble canónico
queda completamente determinado por la expresión anterior y la distribución
de probabilidades, que finalmente toma la forma
La ecuación
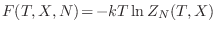 provee toda la información
termodinámica que posee nuestro sistema, pues se trata de la relación
fundamental en la representación de Helmholtz. Esto significa que el
objetivo de nuestra descripción de un sistema en el ensamble canónico se
reduce a encontrar la función partición, ya que de allí se establece toda la
conexión con la teoría termodinámica.
provee toda la información
termodinámica que posee nuestro sistema, pues se trata de la relación
fundamental en la representación de Helmholtz. Esto significa que el
objetivo de nuestra descripción de un sistema en el ensamble canónico se
reduce a encontrar la función partición, ya que de allí se establece toda la
conexión con la teoría termodinámica.
Es interesante destacar el comportamiento del sistema para temperaturas
extremas, según la descripción dada por la expresión anterior. Por un lado,
cuando 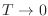 , es decir
, es decir
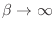 ,
,
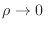 para cualquier
estado excepto el fundamental. Por otro lado, cuando
para cualquier
estado excepto el fundamental. Por otro lado, cuando
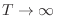 (
(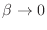 ),
), 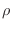 se hace constante, de modo que todos los estados
microscópicos del sistema son igualmente probables: habrá estados con
idéntica energía, pero ningún estado se puebla con preferencia cuando la
temperatura se vuelve lo suficientemente alta.
se hace constante, de modo que todos los estados
microscópicos del sistema son igualmente probables: habrá estados con
idéntica energía, pero ningún estado se puebla con preferencia cuando la
temperatura se vuelve lo suficientemente alta.
Respecto de la expresión que hemos dado para la partición, también vale la
pena enfatizar que deben agotarse todos los estados accesibles para el
sistema, y no solo recorrer los niveles de energía. En otras palabras,
también aquí puede ocurrir que muchos estados compartan la misma energía,
por lo que en la integral involucrada en 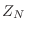 se repetirán muchas
contribuciones idénticas. Suele escribirse la función partición
como
se repetirán muchas
contribuciones idénticas. Suele escribirse la función partición
como
donde 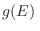 es la densidad de estados en el espacio de las fases con energía
es la densidad de estados en el espacio de las fases con energía 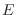 , a menudo llamada degeneración:
, a menudo llamada degeneración:
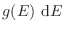 da la probabilidad de que un estado elegido al azar en
da la probabilidad de que un estado elegido al azar en 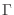 tenga energía entre
tenga energía entre 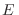 y
y
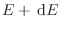 . Con esta notación, en términos de la energía
. Con esta notación, en términos de la energía 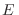 del sistema, la densidad de probabilidad se escribe análogamente como
del sistema, la densidad de probabilidad se escribe análogamente como
Gustavo Castellano 19/11/2021
![$\displaystyle S = - k \int_\Gamma {\rm d}\bm{X}^N\; \rho(\bm{X}^N) \ln [C^N\rho(\bm{X}^N)]\;,
$](img511.png)
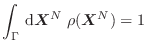
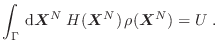
![$\displaystyle \delta\left\{ \int_\Gamma {\rm d}\bm{X}^N \left[ \alpha_o \rho...
...m{X}^N) -k \rho(\bm{X}^N)
\ln [C^N\rho(\bm{X}^N)] \right] \right\} = 0 \;.
$](img516.png)
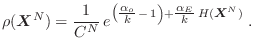
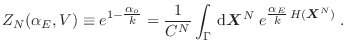

![$\displaystyle \fbox{ $\displaystyle Z_N(T,X) = \frac 1{C^N}
\int_\Gamma \...
...ta H(\mbox{\footnotesize\boldmath $X$}^N)}
\rule[-1.75em]{0em}{4em} $ }
$](img527.png)
![$\displaystyle \fbox{ $\displaystyle \rho(\bm{X}^N) = \frac 1{C^N Z_N(T,X)...
...eta H(\mbox{\footnotesize\boldmath $X$}^N)} \rule[-1.75em]{0em}{4em} $ }
$](img528.png)
![]() , es decir
, es decir
![]() ,
,
![]() para cualquier
estado excepto el fundamental. Por otro lado, cuando
para cualquier
estado excepto el fundamental. Por otro lado, cuando
![]() (
(![]() ),
), ![]() se hace constante, de modo que todos los estados
microscópicos del sistema son igualmente probables: habrá estados con
idéntica energía, pero ningún estado se puebla con preferencia cuando la
temperatura se vuelve lo suficientemente alta.
se hace constante, de modo que todos los estados
microscópicos del sistema son igualmente probables: habrá estados con
idéntica energía, pero ningún estado se puebla con preferencia cuando la
temperatura se vuelve lo suficientemente alta.
![]() se repetirán muchas
contribuciones idénticas. Suele escribirse la función partición
como
se repetirán muchas
contribuciones idénticas. Suele escribirse la función partición
como