Equipartición de la energía

En esta sección analizaremos una propiedad importante de sistemas clásicos para los cuales el hamiltoniano es cuadrático en cada variable del espacio de las fases. Denotando como $x_1,\dots,x_n$ a las componentes de $(\bm{q}^N,\bm{p}^N)$ que intervienen en el hamiltoniano (pueden ser solo algunas de ellas), podemos expresar

$$H(\bm{X}^N) = \sum_{j=1}^n \frac12 \alpha_j x_j^2 \;.$$

Los valores de las constantes $\alpha_j$ ($\neq0$ todas) dependen de la situación particular de que se trate: si $x_j$ representa un momento lineal, entonces $\alpha_j$ corresponde a la recíproca de la masa involucrada, $1/m$; si $x_j$ designa una coordenada generalizada, entonces $\alpha_j$ es la constante elástica asociada a la fuerza generalizada de restitución.

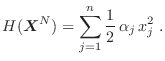
El teorema de equipartición de la energía puede enunciarse de la siguiente manera:

En otras palabras, $U\!=\!nkT/2$, es decir la energía está igualmente distribuida en cada grado de libertad, y es proporcional a la temperatura. La demostración del teorema es muy sencilla, ya que la función partición se escribe como

$$Z_N = \frac 1{C^N} \int_\Gamma {\rm d}\bm{X}^N \; e^{-{\textst... ...alpha_j x_j^2} = B(N,X) \prod_{j=1}^n \sqrt{\frac{2\pi}{\beta\alpha_j}} \;.$$

La función $B(N,X)$ resulta de integrar aquellas $q$ y $p$ que no intervienen en el hamiltoniano, y esencialmente aquí nos interesa que no depende de la temperatura. Dejando como ejercicio probar que $U\!=\!-\partial(\ln Z_N)/\partial\beta$, puede utilizarse esta identidad para ver que

$$U = \frac{\partial }{\partial\beta}\left(\sum_{j=1}^n\ln\sqrt{\beta}\right) = \frac n2 kT \;,$$

que es lo que se deseaba demostrar. A menudo el teorema de equipartición se verifica al analizar los calores específicos, que satisfacen la relación

$$N c_X = \left(\frac{\partial U}{\partial T}\right)_{X,N} = \frac{nk}2\;.$$

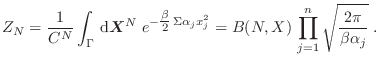
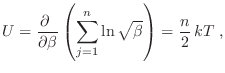
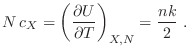
Para considerar algunos ejemplos sencillos, recurrimos primero al caso del gas ideal, cuyo hamiltoniano involucra los $3N$ impulsos lineales. Se deja como ejercicio ver que la función partición resulta

$$Z_N(T,V) = \frac{V^N}{C^N} (2\pi mkT)^{3N/2} \;,$$

con lo cual

$$U = \frac32 NkT \qquad;\qquad\qquad c_V = \frac32 k \;.$$

Este resultado coincide con el previsto por el teorema de equipartición de la energía, ya que en este caso los grados de libertad $x_j$ del enunciado anterior son los $3N$ impulsos lineales.

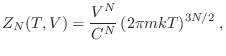
En el caso de moléculas diatómicas clásicas, a los grados de libertad traslacionales deben agregarse las rotaciones, que a temperatura ambiente están presentes y pueden ser descriptas clásicamente. El hamiltoniano clásico suma entonces dos términos cuadráticos a cada molécula, que involucran los impulsos generalizados correspondientes a las dos coordenadas angulares que determinan la orientación de la molécula. La energía interna agrega ahora la contribución de estos $2N$ términos, de modo que $U\!=\!5NkT/2$. Cuando además se activan los modos vibracionales, en el hamiltoniano se incorporan dos términos cuadráticos por molécula, pues las oscilaciones pueden separarse del movimiento del centro de masa mediante la coordenada relativa y el impulso generalizado correspondiente. De este modo, la energía interna resulta en este caso igual a $7NkT/2$.