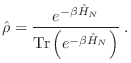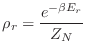Descripción cuántica

Para desarrollar la mecánica estadística desde un enfoque cuántico, el procedimiento es similar al del caso clásico. Ahora debe maximizarse la entropía

$$S=-k {\rm Tr} (\hat\rho \ln\hat\rho)$$

recurriendo a las expresiones adecuadas para los vínculos

$${\rm Tr} \hat\rho = 1 \qquad\qquad {\rm y} \qquad\qquad {\rm Tr} (\hat H_N \hat\rho) = U \;.$$

Se deja como ejercicio verificar que si acompañamos los vínculos con los mismos multiplicadores de Lagrange que en la sección anterior, la condición de máximo implica

$${\rm Tr} \left\{ \delta\hat\rho \left[ (\alpha_o-k)\hat I + \alpha_E \hat H_N - k \ln\hat\rho \right] \right\} = 0 \;.$$

También en este caso esta igualdad debe cumplirse para cualquier variación 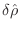$\delta\hat\rho$, de modo que arribamos a las siguientes expresiones análogas a las del caso clásico:

$$Z_N(T,X) = {\rm Tr} \left(e^{-\beta\hat H_N}\right) \quad; \qquad\qquad F(T,X,N) = -kT \ln Z_N(T,X) \;.$$

La solución para el operador densidad resulta

$$\hat\rho = \frac{e^{-\beta\hat H_N}} {{\rm Tr} \left(e^{-\beta\hat H_N}\right)} \;.$$

En caso de tener una representación diagonal⁸, el elemento 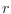$r$-ésimo de 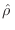$\hat\rho$ se escribe

$$\rho_r = \frac{e^{-\beta E_r}}{Z_N}$$

y representa la probabilidad de que el sistema se encuentre en el estado 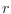$r$.⁹