Fluctuaciones de la energía

Ahora que hemos desarrollado el formalismo correspondiente al ensamble canónico vale la pena preguntarnos en qué cambiará la descripción termodinámica provista desde este formalismo en relación a la dada en el ensamble microcanónico. Para ello es útil analizar cuánto puede fluctuar la energía de nuestro sistema al considerar en el ensamble canónico.

A partir de la expresión

$${\rm Tr} \left\{ e^{\beta\left[F(T,X,N)-\hat H_N\right]} \right\} = 1$$

derivamos con respecto a $\beta$ y obtenemos

$${\rm Tr} \left\{ \left[ \left(\frac{\partial \beta F}{\partial \beta}\right)_{X,N} - \hat H_N \right] e^{\beta(F-\hat H_N)} \right\} = 0 \;.$$

Derivando nuevamente, llegamos a la relación

$${\rm Tr} \left\{ \left[ \left(\frac{\partial^2 \beta F}{\partia... ...t)_{X,N} - \hat H_N \right)^2 \right] e^{\beta(F-\hat H_N)} \right\} = 0 \;.$$

Recordando que $\partial(\beta F)/\partial\beta\!=\!\langle E\rangle$, vemos que las fluctuaciones de la energía se rigen según

$$\langle E^2\rangle - \langle E\rangle^2 = - \left(\frac{\partial... ...X,N} = - \left(\frac{\partial U}{\partial\beta}\right)_{X,N} = kT^2N c_x \;.$$

Como $\langle E\rangle\!=\!U$ es extensiva y por ende proporcional a $N$, en el límite termodinámico

$$\frac{\sqrt{\langle E^2\rangle - \langle E\rangle^2}}{\langle E\rangle} \sim \frac 1{\sqrt{N}} \to 0 \;.$$

Esto significa que las fluctuaciones relativas de la energía son muy pequeñas cuando $N\to\infty$, lo que implica que los únicos estados del sistema con probabilidad no nula son aquellos con $E\cong U$. Esto nos permite concluir que el ensamble canónico es equivalente al microcanónico, y la elección de uno u otro ensamble quedará supeditada a la conveniencia de la descripción en el formalismo escogido.

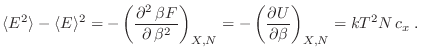
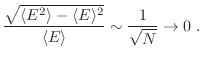
Físicamente podíamos prever esta equivalencia, ya que es idéntico pensar que prefijamos los valores de $U$, $X$ y $N$ (ensamble microcanónico) y procuramos el valor de $T$ a través de una ecuación de estado (por ej., en la representación entropía), o imaginar que conocemos $T$, $X$ y $N$ (ensamble canónico) y de la relación fundamental obtenemos el valor de $U$ en el equilibrio. La situación termodinámica no cambia en absoluto, aunque los microestados permitidos para el sistema ahora pueden abarcar diferentes energías.