Siguiente: Definición de probabilidad Subir: Probabilidad Anterior: Probabilidad
Cuando trabajamos con muchos objetos, estos conceptos aparecen frecuentemente. Una permutación es un arreglo de un conjunto de ![]() objetos diferentes en un orden definido. El número de permutaciones diferentes de estos
objetos diferentes en un orden definido. El número de permutaciones diferentes de estos ![]() objetos es
objetos es ![]() ; esto se ve fácilmente si pensamos que para la primera alternativa disponemos de los
; esto se ve fácilmente si pensamos que para la primera alternativa disponemos de los ![]() elementos del conjunto, cada uno de los cuales puede complementarse con los
elementos del conjunto, cada uno de los cuales puede complementarse con los ![]() restantes como segunda opción, y así hasta llegar a la última elección, conformando el producto
restantes como segunda opción, y así hasta llegar a la última elección, conformando el producto
![]() .
.
El número de permutaciones posibles al tomar ![]() objetos del conjunto de
objetos del conjunto de
![]() elementos será, siguiendo el mismo razonamiento,
elementos será, siguiendo el mismo razonamiento,
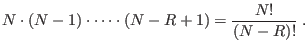
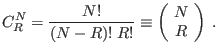
Si un conjunto de ![]() elementos contiene
elementos contiene ![]() elementos idénticos de tipo
1,
elementos idénticos de tipo
1, ![]() de tipo 2,
de tipo 2, ![]() ,
, ![]() de tipo
de tipo ![]() , puede verse que el
número de permutaciones posibles será
, puede verse que el
número de permutaciones posibles será

Gustavo Castellano 19/11/2021