Siguiente: Variables aleatorias o estocásticas Subir: Probabilidad Anterior: Permutaciones y combinaciones
Aceptamos como probabilidad nuestra expectativa respecto del
resultado de un experimento o “evento”. Si un posible resultado de cierto
experimento es ![]() , su probabilidad es
, su probabilidad es ![]() si al realizar
si al realizar ![]() experimentos idénticos esperamos que el resultado
experimentos idénticos esperamos que el resultado ![]() se obtenga en
se obtenga en
![]() de ellos. Dicho de otra manera, a medida que
de ellos. Dicho de otra manera, a medida que
![]() ,
esperamos que la fracción de eventos con resultado
,
esperamos que la fracción de eventos con resultado ![]() tienda a
tienda a ![]() .
.
Un ejemplo sencillo pero que encontraremos muy frecuentemente es el de ![]() resultados igualmente probables de los cuales
resultados igualmente probables de los cuales ![]() corresponden al caso
corresponden al caso
![]() que nos interesa: en ese caso,
que nos interesa: en ese caso, ![]() .
.
Definimos espacio muestral asociado a un determinado experimento
como el conjunto ![]() constituido por todos los resultados posibles de ese
experimento. Un evento plausible entonces corresponderá a un subconjunto de
constituido por todos los resultados posibles de ese
experimento. Un evento plausible entonces corresponderá a un subconjunto de
![]() .
.
Utilizando el lenguaje de teoría de conjuntos, denotamos como ![]() a la unión de
a la unión de ![]() y
y ![]() , que es
el conjunto de todos los puntos que pertenecen a
, que es
el conjunto de todos los puntos que pertenecen a ![]() o a
o a ![]() (o a
ambos). La intersección
(o a
ambos). La intersección ![]() de estos conjuntos se define
como el conjunto de todos los puntos que pertenecen a
de estos conjuntos se define
como el conjunto de todos los puntos que pertenecen a ![]() y a
y a ![]() simultáneamente. Si
simultáneamente. Si
![]() (no contiene puntos),
(no contiene puntos), ![]() y
y
![]() son mutuamente excluyentes.
son mutuamente excluyentes.
Algunas probabilidades que resultan evidentes, en esta notación se expresan como
Si
![]() son mutuamente excluyentes y exhaustivos, es
decir, cubren todo el espacio muestral y por lo tanto
son mutuamente excluyentes y exhaustivos, es
decir, cubren todo el espacio muestral y por lo tanto
![]() , decimos que
, decimos que ![]() es una partición de
es una partición de ![]() en
en ![]() subconjuntos. Cuando
subconjuntos. Cuando ![]() es una partición se cumple que
es una partición se cumple que
![]() .
.
Dos observaciones diferentes ![]() y
y ![]() (pueden ser de eventos similares o completamente distintas) son eventos independientes si y sólo si
(pueden ser de eventos similares o completamente distintas) son eventos independientes si y sólo si
![]() . Aquí es importante destacar que en esta notación,
. Aquí es importante destacar que en esta notación, ![]() corresponde al resultado
corresponde al resultado ![]() permitiendo cualquier evento
permitiendo cualquier evento ![]() , y análogamente para el resultado
, y análogamente para el resultado ![]() .
.
Se define probabilidad condicional ![]() como la probabilidad de
obtener el resultado
como la probabilidad de
obtener el resultado ![]() dado que también se obtiene
dado que también se obtiene ![]() :
:
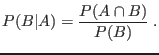
Gustavo Castellano 19/11/2021