Descripción clásica

Hemos visto que la expresión clásica para la función partición

$$Z_N(T,X) = \frac 1{C^N} \int_\Gamma {\rm d}\bm{X}^N \; e^{-\beta H(\mbox{\footnotesize\boldmath$X$}^N)}$$

provee una correcta conexión con la termodinámica en el caso de un gas ideal, verificándose además el teorema de equipartición de la energía. Para analizar el caso de las oscilaciones colectivas de una red cristalina, debemos recordar que los $3N$ osciladores acoplados pueden describirse mediante coordenadas normales como un sistema de $3N$ osciladores armónicos desacoplados (modos normales)

$$H(\bm{X}^N) = \sum_{i=1}^{3N} \left( \frac{1}{2m} p_i^2 + \frac{m\omega_i^2}2 x_i^2 \right) \;.$$

La integración de la función partición es directa, teniendo en cuenta que todas las coordenadas e impulsos $x_i$ y $p_i$ son independientes:

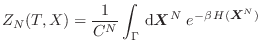
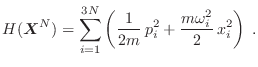
$$Z_N(T,V) = \frac1{h^{3N}} \int {\rm d}\bm{x}^{3N} {\rm d}\bm{p}... ...e\left( \frac{1}{2m} p_i^2 + \frac{m\omega_i^2}2 x_i^2 \right)} \right] \;.$$

El hecho de que los osciladores sean independientes se traduce en la factorización de la función partición como producto de las “particiones individuales” $z_i$ correspondientes a cada oscilador. Esta factorización podrá realizarse en todo sistema que pueda separarse en componentes no interactuantes. En nuestro caso particular las “particiones individuales” se calculan mediante la expresión

$$z_i = \frac 1 h \int_{-\infty}^{+\infty} {\rm d}p\; e^{-\beta\... ...L/2}^{+L/2} {\rm d}x\; e^{-\beta{\textstyle\frac{m\omega_i^2}{2}} x^2} \;.$$

Como la exponencial decae rápidamente para posiciones alejadas del equilibrio, podemos realizar la segunda integración entre $-\infty$ y $+\infty$, de manera que

$$z_i = \frac 1 h \sqrt{2\pi mkT} \sqrt{\frac{2\pi kT}{m\omega_i^2}} = \frac{2\pi}{h\omega_i} kT \;.$$

Entonces, independientemente de los valores que puedan tomar los $\omega_i$, la descripción clásica del sólido cristalino predice que

$$U = 3NkT \qquad\qquad {\rm y} \qquad\qquad c_v = 3k \;.$$

Estos resultados podrían haberse predicho mediante el teorema de equipartición de la energía.

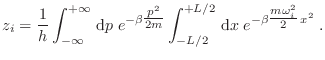
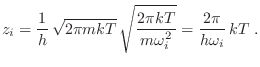
Vemos que esta descripción no reproduce satisfactoriamente el comportamiento para bajas temperaturas, pues el calor específico de un sólido debe anularse a medida que se reduce su temperatura, tal como se deduce a partir de consideraciones cuánticas. A temperaturas altas los estados más energéticos del oscilador cuántico se pueblan cada vez más, de manera que la correspondiente “distribución de presencia” se hace cada vez más parecida a la predicha por la clásica.

Para aclarar un poco esta idea recordemos que mientras la probabilidad de encontrar a la partícula clásica que oscila es proporcional a la inversa de la velocidad $v(x)$

$$P_{\mbox{\footnotesize clás}}(x) \propto \frac1{\vert v(x)\vert} = \frac1{+\omega\sqrt{x_o^2-x^2}} \;,$$

donde $x_o$ es el punto de retorno clásico, la correspondiente probabilidad cuántica es el módulo de la función de onda al cuadrado $\vert\psi_n(x)\vert^2$. Para los primeros estados cuánticos, esta probabilidad se parece muy poco a la del oscilador clásico, tal como se muestra en la figura (aquí se ha normalizado el rango de coordenadas espaciales para que coincidan los puntos de retorno clásico.)

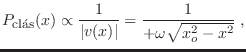
Para estados con $n$ mayor, la distribución $\vert\psi_n(x)\vert²$ se parece cada vez más a $P_{\mbox{\footnotesize clás}}(x)$, por lo cual ambas descripciones pueden resultar adecuadas a temperaturas altas, pero no a bajas temperaturas donde se privilegian los estados de menor energía.