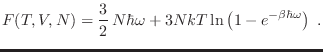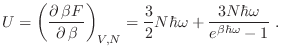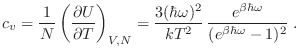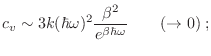La descripción cuántica retoma la idea de 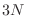 osciladores desacoplados
(distinguibles), para los cuales los autovalores de los hamiltonianos
osciladores desacoplados
(distinguibles), para los cuales los autovalores de los hamiltonianos
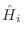 resultan
resultan
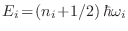 , o bien, en
términos del operador número,
, o bien, en
términos del operador número,
(Podemos pensar que el operador número se define a partir de esta relación,
y se satisface que
![$[\hat H_i,\hat n_i]\!=\!0 $](img610.png) y
y
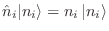 ).
).
Dijimos que el modelo de Einstein consiste en hacer
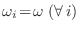 , de manera que obtenemos
, de manera que obtenemos
Como las funciones de onda conjuntas que describen a los 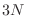 osciladores
independientes son simplemente productos tensoriales
osciladores
independientes son simplemente productos tensoriales
la expresión para la partición se evalúa fácilmente en esta base, utilizando
el hecho de que las funciones de onda individuales son ortonormales
(
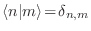 ):
):
es decir
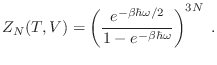 |
(14) |
Podemos entonces expresar la energía libre de Helmholtz como
El primer término representa la energía libre a 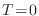 , y no es cero, tal
como lo predice el principio de incertidumbre de Heisenberg. Se sugiere como
ejercicio verificar que esta expresión satisface la tercera ley de la
termodinámica (
, y no es cero, tal
como lo predice el principio de incertidumbre de Heisenberg. Se sugiere como
ejercicio verificar que esta expresión satisface la tercera ley de la
termodinámica (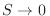 para
para 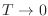 ).
).
Podemos evaluar la energía interna a partir de la expresión anterior:
El ingenuoso lector no dudará en verificar fácilmente que esta expresión
reproduce los resultados clásicos para temperaturas elevadas; para 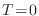 , la
energía interna nuevamente está dada por el primer término.
, la
energía interna nuevamente está dada por el primer término.
También puede obtenerse el calor específico por núcleo
En el régimen de bajas temperaturas, es decir, pensando
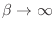 , el
comportamiento asintótico está dado por
, el
comportamiento asintótico está dado por
para temperaturas altas (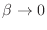 ), al tomar el límite surgen un par de
indeterminaciones que se resuelven mediante la regla de L'Hôpital, y puede
verificarse (¡tú puedes hacerlo!) que se obtiene el comportamiento clásico
), al tomar el límite surgen un par de
indeterminaciones que se resuelven mediante la regla de L'Hôpital, y puede
verificarse (¡tú puedes hacerlo!) que se obtiene el comportamiento clásico
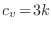 . Por supuesto, los comportamientos para temperaturas altas podían
predecirse recurriendo al teorema de equipartición de la energía.
. Por supuesto, los comportamientos para temperaturas altas podían
predecirse recurriendo al teorema de equipartición de la energía.
Gustavo Castellano 19/11/2021
![]() osciladores desacoplados
(distinguibles), para los cuales los autovalores de los hamiltonianos
osciladores desacoplados
(distinguibles), para los cuales los autovalores de los hamiltonianos
![]() resultan
resultan
![]() , o bien, en
términos del operador número,
, o bien, en
términos del operador número,
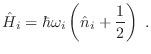
![]() , de manera que obtenemos
, de manera que obtenemos
![$\displaystyle Z_N = \sum_{n_1=0}^\infty \cdots \sum_{n_{3N}=0}^\infty
e^{-\bet...
.../2}
\sum_{n_i=0}^\infty \left(e^{-\beta\hbar\omega}\right)^{n_i}\right] \;,
$](img616.png)