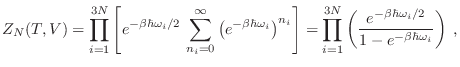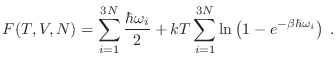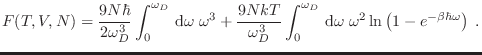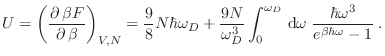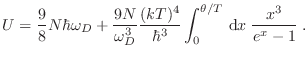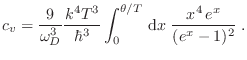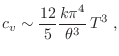Aunque cualitativamente la descripción dada por el modelo de Einstein es correcta, de acuerdo con los resultados experimentales 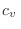 no debería decaer exponencialmente cuando
no debería decaer exponencialmente cuando
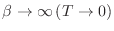 . Este inconveniente se resuelve evitando la simplificación de frecuencias idénticas para todos los modos normales:
. Este inconveniente se resuelve evitando la simplificación de frecuencias idénticas para todos los modos normales:
La idea de Debye fue suponer que los osciladores “conforman” una red de
dimensiones características
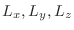 , de modo que las longitudes de
onda
, de modo que las longitudes de
onda  permitidas en estas oscilaciones serán
permitidas en estas oscilaciones serán
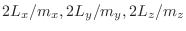 , con
, con
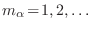 Admitiendo que
entre las frecuencias
Admitiendo que
entre las frecuencias 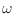 y los vectores de onda
y los vectores de onda 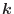 , con
, con
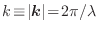 , la
relación de dispersión unidimensional es
, la
relación de dispersión unidimensional es
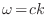 , donde
, donde 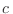 es la
velocidad del sonido en el medio, en tres dimensiones tendremos
es la
velocidad del sonido en el medio, en tres dimensiones tendremos
(estas son las 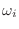 que teníamos en la expresión anterior: por supuesto, algunas ternas
que teníamos en la expresión anterior: por supuesto, algunas ternas
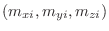 definen frecuencias repetidas).
Dado que el límite termodinámico implica
definen frecuencias repetidas).
Dado que el límite termodinámico implica
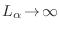 , estas
, estas
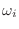 pueden tomarse como variables continuas. En el espacio
pueden tomarse como variables continuas. En el espacio 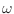 ,
la distancia según cada coordenada
,
la distancia según cada coordenada 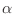 es
es
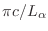 , de modo
que el volumen correspondiente a cada modo será
, de modo
que el volumen correspondiente a cada modo será
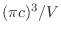 . Si
. Si 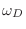 es la frecuencia máxima posible, el volumen del octavo de esfera de radio
es la frecuencia máxima posible, el volumen del octavo de esfera de radio
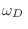 (
(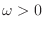 ) dividido el volumen correspondiente a un estado
es igual al número de modos normales posibles
) dividido el volumen correspondiente a un estado
es igual al número de modos normales posibles
En realidad, hay en general 3 modos normales posibles con cada 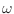 :
uno longitudinal y dos transversales, con diferentes
velocidades de propagación,
:
uno longitudinal y dos transversales, con diferentes
velocidades de propagación, 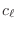 y
y 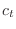 . La igualdad anterior debe
escribirse entonces como la suma de los modos transversales más el longitudinal para totalizar los
. La igualdad anterior debe
escribirse entonces como la suma de los modos transversales más el longitudinal para totalizar los 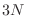 modos normales
modos normales
La frecuencia
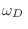 se denomina frecuencia de Debye. La expresión anterior es también válida para obtener el número de modos
se denomina frecuencia de Debye. La expresión anterior es también válida para obtener el número de modos
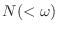 con frecuencias menores que cualquier
con frecuencias menores que cualquier 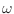
de manera que el número de modos con frecuencias entre 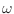 y
y
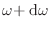 es
es
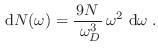 |
(15) |
Volviendo a la función partición, la expresión que reemplaza a la
ecuación (14) es
de modo que tendremos
Teniendo presente que los valores de 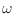 se tornan continuos, y utilizando la identidad (15), podemos hacer el reemplazo de sumatorias por integrales obteniendo la expresión
se tornan continuos, y utilizando la identidad (15), podemos hacer el reemplazo de sumatorias por integrales obteniendo la expresión
El primer término se integra directamente, y para la energía interna puede escribirse
Sustituyendo
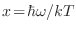 podemos escribir la expresión anterior en términos de la temperatura de Debye10
podemos escribir la expresión anterior en términos de la temperatura de Debye10
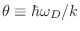
La expresión para el calor específico resulta entonces
Nuevamente, la predicción para altas temperaturas coincide con la clásica,
pero la diferencia fundamental con el modelo de Einstein se da para bajas
temperaturas, pues en ese caso
describiendo adecuadamente el comportamiento de las determinaciones
experimentales.
Gustavo Castellano 19/11/2021
![]() no debería decaer exponencialmente cuando
no debería decaer exponencialmente cuando
![]() . Este inconveniente se resuelve evitando la simplificación de frecuencias idénticas para todos los modos normales:
. Este inconveniente se resuelve evitando la simplificación de frecuencias idénticas para todos los modos normales:
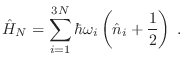
![$\displaystyle \omega_i^2 = c^2 \left[ \left(\frac{\pi m_{xi}}{L_x}\right)^2 +
...
...rac{\pi m_{yi}}{L_y}\right)^2 + \left(\frac{\pi m_{zi}}{L_z}\right)^2 \right]
$](img635.png)
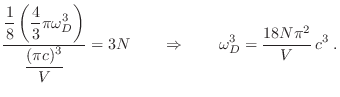
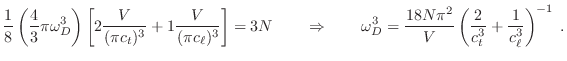
![$\displaystyle N(<\omega) = \frac{1}{8}\left(\frac{4}{3}\pi\omega^3\right)
\lef...
...3} + 1\frac{V}{(\pi c_\ell)^3} \right] =
\frac{3N}{ \omega_D^3} \omega^3 \;,
$](img649.png)