Moléculas diatómicas: el caso del hidrógeno (basado en el texto de Balian)

El análisis de las moléculas diatómicas resulta de especial interés porque permite avanzar en la comprensión de diferentes situaciones. Para ello, consideramos las moléculas de un gas diatómico como rotadores rígidos, conformados por dos átomos puntuales mantenidos a distancia fija. A temperatura ambiente, los grados de libertad electrónicos y de vibración no están excitados, de manera que esta aproximación resulta muy adecuada.

Los grados de libertad traslacionales se corresponden con los de una partícula cuántica en una caja (tridimensional) de lado $a$, de modo que los niveles de energía estarán dados por $[h^2/(8ma^2)](k^2\!+\!\ell^2\!+\!m²)$ ( $k,\ell,m\;\epsilon\;\mathbb{Z} \ge0$). Para una masa atómica del orden de 10$^{-23 }$g y una caja de lado $a\!=\!1$cm, la energía térmica relacionada con el salto entre dos niveles consecutivos de energía corresponde a una temperatura de 10$^{-14 }$K, de modo que a temperatura ambiente, la contribución de los modos traslacionales a la energía interna puede calcularse mediante un enfoque clásico.

Nos concentramos entonces en la energía cinética de rotación, cuya expresión clásica, en términos del momento de inercia $I$ es

$$\frac{p_\theta^2}{2 I} + \frac{p_\phi^2}{2 I {\rm sen}^2\theta}\;.$$

Para masas $m_1$ y $m_2$, si $r_o$ es la distancia entre ambas, resulta

$$\hspace{18em} I = \frac{m_1 m_2}{m_1+m_2} r_o^2 \;.$$

Sabemos que los niveles de energía para un rotador cuántico se traducen directamente como

$$\hspace{40em} \epsilon_j = \frac{\hbar^2}{2 I} j(j+1) \;,$$

con degeneración $g_j\!=\!2j\!+\!1$. Definiendo la temperatura rotacional $\Theta\!\equiv\!\hbar^2/(2Ik)$, la función partición por molécula estará dada por

$$Z_1 = \sum_{j=0}^\infty (2j+1) e^{-j(j+1) \Theta/T} \;.$$

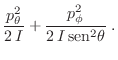
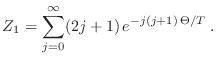
Para el caso $T\gg\Theta$, podemos hacer la sustitución $x\!=\!j(j\!+\!1)\Theta/T$, resultando una variable continua en este rango de temperaturas. De este modo, obtenemos

$$\hspace{30em} Z_1 \approx \frac T\Theta \int_0^\infty {\rm d}x\; e^{-x} = \frac T\Theta \;.$$

Si en cambio $T\ll\Theta$, tenemos

$$Z_1 \approx 1 + 3 e^{-2\Theta/T} + 5 e^{-6\Theta/T} + \dots$$

Así, para la energía media por molécula $\bar\epsilon\!=\!-\partial(\ln Z_1)/\partial\beta$ encontramos:

$$\cdot\quad T\gg\Theta:\quad \bar\epsilon = kT \hspace{12.5em}$$

$$\cdot\quad T\ll\Theta:\quad \bar\epsilon = k\Theta \left[ 6 e^{-2\Theta/T} - 18 e^{-4\Theta/T} + \dots \right]$$

De este modo, los calores específicos resultan

$$\cdot\quad T\gg\Theta:\quad c_v = k \hspace{16em}$$

$$\cdot\quad T\ll\Theta:\quad c_v = k \left(\displaystyle\frac{\Theta}T\right)^2 \left[ 12 e^{-2\Theta/T} - 72 e^{-4\Theta/T} + \dots \right]$$

Para el caso de la molécula de hidrógeno, los valores predichos para $c_v$ sobreestiman demasiado los valores experimentales. Esta discrepancia no se debe al hecho de haber despreciado las energías de vibración y estados electrónicos excitados, no solo porque la diferencia se notaría únicamente a $T$ muy altas, sino porque además en ese caso la predicción debería ir por debajo de las mediciones (pues faltaría agregar alguna contribución a $c_v$). En cambio, lo que no se ha tenido en cuenta es el espín 1/2 de los núcleos de hidrógeno, ni tampoco el hecho de que el espín total $\sigma$ de las moléculas puede ser 0 (núcleos antiparalelos) o 1 (paralelos). El para-estado ( $\sigma\!=\!0$) tiene degeneración $2\sigma\!+\!1\!=\!1$, mientras que el orto-estado ( $\sigma\!=\!1$) tiene degeneración 3.

Cuando los átomos son distintos, en muy buena aproximación, la degeneración de cada estado no influye en el valor de la energía, porque esta será casi independiente de $\sigma$. En ese caso, la función partición debe multiplicarse por un factor constante $(2s_1\!+\!1)(2s_2\!+\!1)$ ( $=\!4$ en nuestro caso).

Sin embargo, cuando los átomos son idénticos, debe tenerse en cuenta la indistinguibilidad de las partículas. El postulado de simetrización exige que la función de onda conjunta de la molécula sea antisimétrica al intercambiar los átomos. Las partes correspondientes a vibración y a estados electrónicos son simétricas en el estado base (no están excitadas). En el para-estado, la función de onda de espín es antisimétrica, mientras que en el orto-estado es simétrica. La función de onda rotacional es simétrica o antisimétrica según el número cuántico $j$ sea par o impar ¹¹. O sea que tendremos:  

para-hidrógeno ( $\sigma\!=\!0$):	$j=0,2,4,\dots$	degeneración 1;
orto-hidrógeno ( $\sigma\!=\!1$):	$j=1,3,5,\dots$	degeneración 3.

Así, la función partición debe calcularse teniendo en cuenta que debe sumarse sobre todos los estados posibles:

$$Z_1 = Z_{\rm para} + 3 Z_{\rm orto} \;,$$

donde $Z_{\rm para}$ abarca los $j$ pares y $Z_{\rm orto}$, los $j$ impares. Teniendo en cuenta todos estos aspectos, la predicción para $c_v$ sigue estando para el para. La solución definitiva se basa en analizar la razón de moléculas en ambos estados

$$r = \frac{N_{\rm orto}}{N_{\rm para}} = \frac{\displaystyle 3 \s... ...heta/T}} {\displaystyle 1 \sum_{j\;{\rm par}} (2j+1) e^{-j(j+1)\Theta/T}} \;.$$

Según esta expresión, cuando $T\to0$, $r\to0$, y cuando $T\gg\Theta$, $r\!=\!3$ (para calcularla, es válido el reemplazo de la sumatoria por una integral tanto en el numerador como en el denominador). A temperatura ambiente, $r\!=\!3$ pues $T\simeq4\Theta$ ( $\approx4\!\times\!85$K). Al reducir la temperatura, $r$ debería bajar, pero no es esto lo que sucede: la transición entre los estados orto y para involucra la inversión de espines, que tiene una probabilidad sumamente baja de ocurrir, y puede llevar años alcanzar el equilibrio en este sentido. Esto significa que típicamente las determinaciones experimentales se realizan fuera del equilibrio, con $r\!=\!3$. Entonces puede considerarse al sistema como una mezcla de gases independientes, de manera que la contribución al calor específico se computa como la suma de los dos gases

$$c_v = c_v^{\rm para} + c_v^{\rm orto} \;.$$

Ahora sí, las predicciones concuerdan con el experimento.

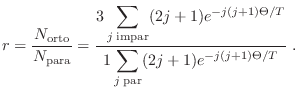
Hay otras alternativas para verificar que el cálculo mediante este método es correcto. Una de ellas es medir el calor específico de mezclas con diferentes valores para $r$. Para hacerlo, el gas se prepara pasándolo por un catalizador (carbono activado) a diferentes temperaturas, con el objeto de acelerar la transición orto-para: en esos experimentos las predicciones concuerdan con los datos medidos.

Las mismas consideraciones que hemos hecho valen para el deuterio diatómico D$_2$. En el caso del HD, por supuesto, no surgen inconvenientes, ya que los dos átomos son diferentes y las cuentas con que comenzamos eran válidas.