Consideremos ahora el caso en que el sistema analizado, además de estar en
contacto con un baño térmico, se encuentra bajo un campo 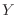 constante, la
variable intensiva relacionada con el trabajo externo. Tendremos que agregar
ahora un nuevo vínculo al maximizar la entropía de información,
correspondiente a mantener el valor medio
constante, la
variable intensiva relacionada con el trabajo externo. Tendremos que agregar
ahora un nuevo vínculo al maximizar la entropía de información,
correspondiente a mantener el valor medio
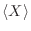 de la variable
extensiva constante.
de la variable
extensiva constante.
Los siguientes ejemplos se encuadran dentro de esta situación:
- gas en un recipiente a
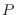 constante
constante 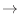 se impone el vínculo
sobre el valor medio
se impone el vínculo
sobre el valor medio
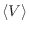 del volumen en el recipiente;
del volumen en el recipiente;
- sustancia magnética (o dieléctrica) a inducción externa
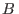 (campo
eléctrico
(campo
eléctrico 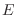 ) constante
) constante 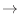 debe considerarse la restricción
de momento magnético total
debe considerarse la restricción
de momento magnético total 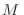 (polarización eléctrica
(polarización eléctrica
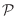 ) constante;
) constante;
- cadena (molecular) a tensión constante
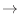 la magnitud
macroscópica que debe agregarse como vínculo es la longitud media
la magnitud
macroscópica que debe agregarse como vínculo es la longitud media
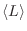 .
.
Para afianzar ideas vamos a abordar el ejemplo concreto de sistemas
magnéticos bajo inducción externa 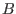 . En el caso de que los núcleos
interactúen entre ellos, una descripción sencilla del hamiltoniano del
sistema acoplado con el campo externo corresponde al denominado modelo
de Ising, cuyos autovalores son
. En el caso de que los núcleos
interactúen entre ellos, una descripción sencilla del hamiltoniano del
sistema acoplado con el campo externo corresponde al denominado modelo
de Ising, cuyos autovalores son
donde las magnitudes
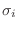 corresponden a los autovalores de los operadores de espín
corresponden a los autovalores de los operadores de espín 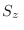 (individuales) según la dirección del campo
(individuales) según la dirección del campo 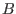 , y
, y
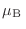 es el
momento magnético correspondiente a cada núcleo --en la discusión que sigue
veremos la importancia de señalar este hamiltoniano como
es el
momento magnético correspondiente a cada núcleo --en la discusión que sigue
veremos la importancia de señalar este hamiltoniano como 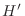 en lugar de
en lugar de
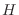 . El cálculo de la función partición nos lleva, como siempre, a recorrer
todos los estados accesibles para el sistema
. El cálculo de la función partición nos lleva, como siempre, a recorrer
todos los estados accesibles para el sistema
y la energía libre de Gibbs queda determinada por
¿Por qué el potencial termodinámico que debe asociarse es el de Gibbs y no
el de Helmholtz? Al maximizar la entropía, además de la condición de
normalización y de fijar
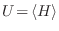 , agregamos el vínculo
, agregamos el vínculo
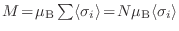 . Dejando los detalles como ejercicio, la identificación que debemos hacer en el proceso variacional, es
. Dejando los detalles como ejercicio, la identificación que debemos hacer en el proceso variacional, es
que es precisamente la energía libre de Gibbs. Para arribar a este
resultado, es necesario distinguir el valor medio del hamiltoniano del
sistema
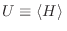 del valor medio
del valor medio
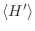 : en
: en
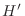 está incluido el campo
está incluido el campo 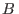 como constante, de manera que cualquier
configuración
como constante, de manera que cualquier
configuración
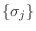 no modifica el valor de
no modifica el valor de 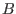 , aunque drene o
entregue energía magnética al enderezar espines. El hecho de que
, aunque drene o
entregue energía magnética al enderezar espines. El hecho de que 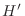 incluya las fuentes de
incluya las fuentes de 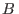 significa que
significa que
es decir, está asociado con la entalpía magnética. Entonces, para el
hamiltoniano “del sistema”, lo correcto es escribir
teniendo la adecuada asociación
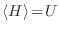 .
.
Conviene hacer hincapié en el hecho de que algunos textos presentan esta
asociación de manera equívoca, refiriendo el potencial termodinámico como
energía libre de Helmholtz; no obstante, se ultilizan siempre las relaciones
En el caso particular de espines no interactuantes,
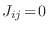 , de manera
que
, de manera
que
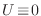 . A diferencia de un gas ideal, al reducir el campo externo el
sistema no guarda para sí ninguna energía, mientras que en el caso del gas, las moléculas conservan la energía mecánica que absorben como energía
cinética.
. A diferencia de un gas ideal, al reducir el campo externo el
sistema no guarda para sí ninguna energía, mientras que en el caso del gas, las moléculas conservan la energía mecánica que absorben como energía
cinética.
Gustavo Castellano 19/11/2021
![]() constante, la
variable intensiva relacionada con el trabajo externo. Tendremos que agregar
ahora un nuevo vínculo al maximizar la entropía de información,
correspondiente a mantener el valor medio
constante, la
variable intensiva relacionada con el trabajo externo. Tendremos que agregar
ahora un nuevo vínculo al maximizar la entropía de información,
correspondiente a mantener el valor medio
![]() de la variable
extensiva constante.
de la variable
extensiva constante.
![]() . En el caso de que los núcleos
interactúen entre ellos, una descripción sencilla del hamiltoniano del
sistema acoplado con el campo externo corresponde al denominado modelo
de Ising, cuyos autovalores son
. En el caso de que los núcleos
interactúen entre ellos, una descripción sencilla del hamiltoniano del
sistema acoplado con el campo externo corresponde al denominado modelo
de Ising, cuyos autovalores son
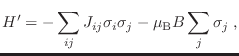
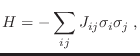

![]() , de manera
que
, de manera
que
![]() . A diferencia de un gas ideal, al reducir el campo externo el
sistema no guarda para sí ninguna energía, mientras que en el caso del gas, las moléculas conservan la energía mecánica que absorben como energía
cinética.
. A diferencia de un gas ideal, al reducir el campo externo el
sistema no guarda para sí ninguna energía, mientras que en el caso del gas, las moléculas conservan la energía mecánica que absorben como energía
cinética.